前言 #

布拉格光栅是一种结构的有效折射率存在周期性变化的光学器件。波导布拉格光栅可以近似一种一维光子晶体结构，通过周期性折射率调制，实现对波长的选择。通常利用这种特性将其制作成各种光学滤波片等。在本案例中，根据 wang 等人的工作可以探究在硅波导布拉格光栅当中，侧壁条纹的几何参数（如深度或者错位）对布拉格光栅性能的影响。

仿真设置 #

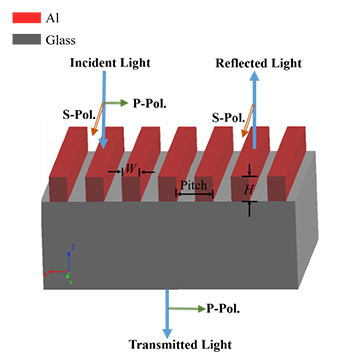
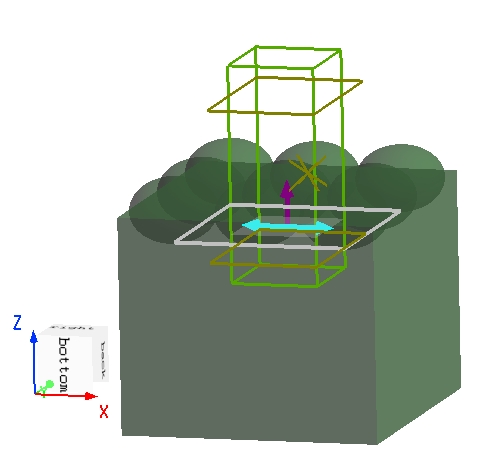
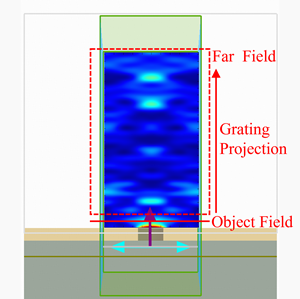
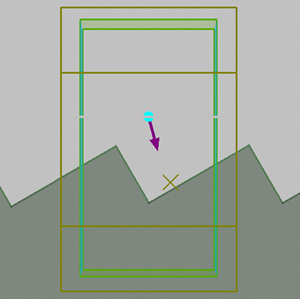
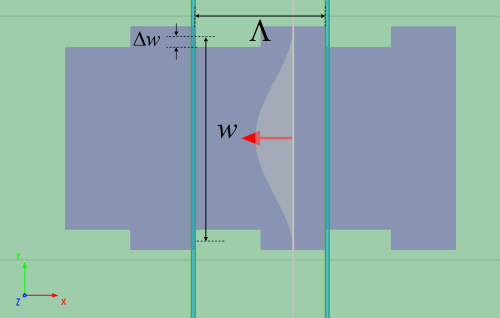
在本案例中，使用 3D FDTD 进行仿真，布拉格光栅是由硅材料组成的光栅器件放置在绝缘硅基平面上组成，其结构详见下图。在 x 方向上设置Bloch边界条件，仿真单个光栅周期，用来模拟无限周期的光栅。图中的结构参数，设置如下，其中 $\Lambda$ 为布拉格光栅单个周期的单元长度， $w$ 为条纹平均宽度， $\Delta w$ 为光栅刻痕的深度。

参数名称	尺寸
$\Lambda$	$0.32 \mu m$
$w$	$0.5 \mu m$
$\Delta w$	$0.05 \mu m$

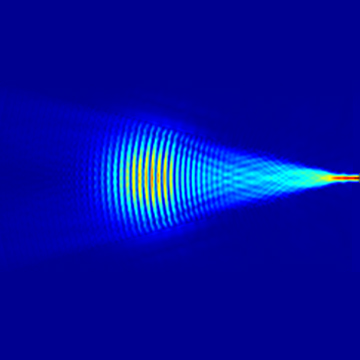
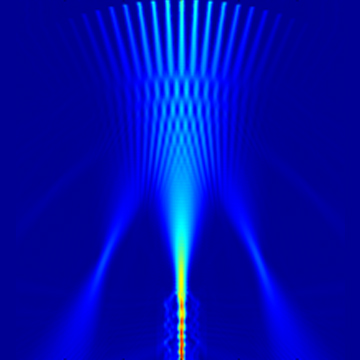
本案例当中光源使用模式光源，其基模 TE0 的场图如下。

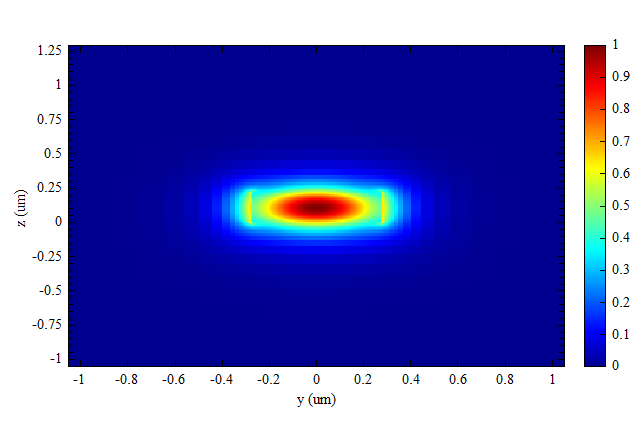
材料设置 #

• 衬底

  本案例中，衬底材料来自软件的内置材料库SiO2(Glass) - Palik, 波长范围在 $1.52\mu m$ ~ $1.56\mu m$，材料的拟合结果如下图所示，在该波段下 $SiO_2$ 的折射率实部和虚部分别为 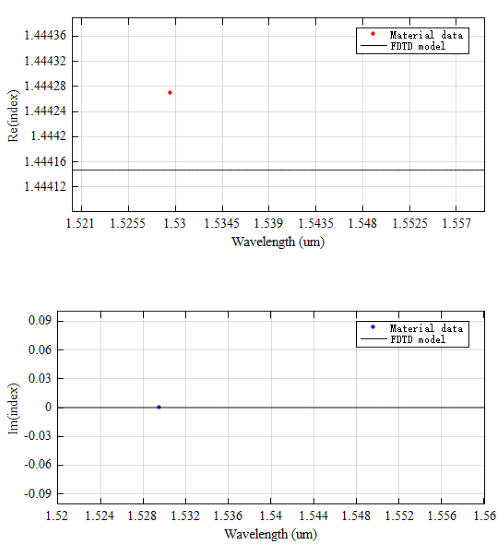$1.44415$ 和 $0$。

  

• 光栅

  光栅材料为 Lorentz 模型建立的 Si 材料，关于 Lorentz 模型的具体细节请参考Drude_Debye_Lorentz。

  $$\varepsilon_{total}(f) =\varepsilon + \frac{\varepsilon_p.\omega_p^2}{\omega_p^2+4\pi j\gamma_p.f-(2\pi f)^2}$$

  本案例中， $\varepsilon = 7.98737$, $\varepsilon_p = 3.68799$, $\omega_p = 3.93282e+15$, $\gamma_p = 1e+8$，此时 $Si$ 材料的折射率实部和虚部如下图所示：

  

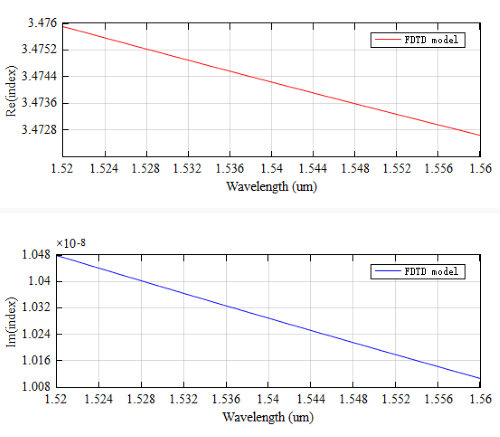
仿真结果 #

本案例中bandstructure可以计算布拉格光栅的光谱。运行结束后，该分析组会得到光栅在波矢 $k_x=\pi/\Lambda$ 时的光谱。打开附录工程文件，直接运行，在bandstructure结果中，即可得到刻痕深度为 $0.05\mu m$ 时，布拉格光栅的能带光谱，如下图所示

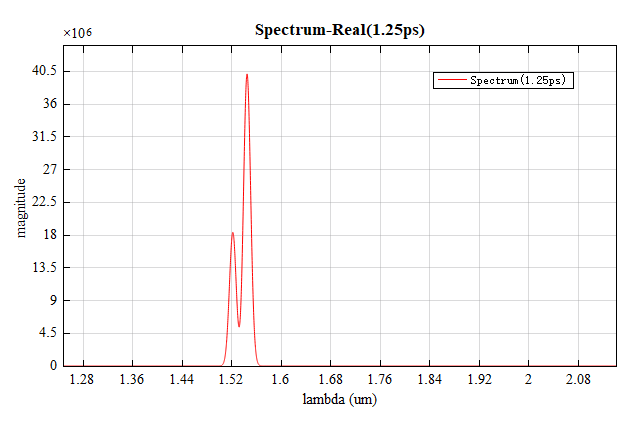
值得注意的是，光谱中共振峰的宽度与计算时间密切相关。计算时间越长，谐振越强，其峰值越尖。对于侧壁刻痕较浅的光栅结构，需要增加计算时间以区分光谱当中不同的共振峰。本案例工程当中初始时间设置为 $1.25ps$。逐渐增加计算时间会使得共振峰的宽度减小，如下图所示，上图计算时间为 $2.5ps$，下图为 $3.75ps$。

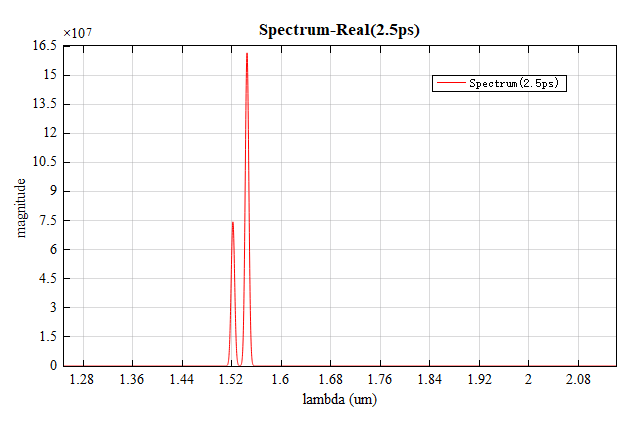
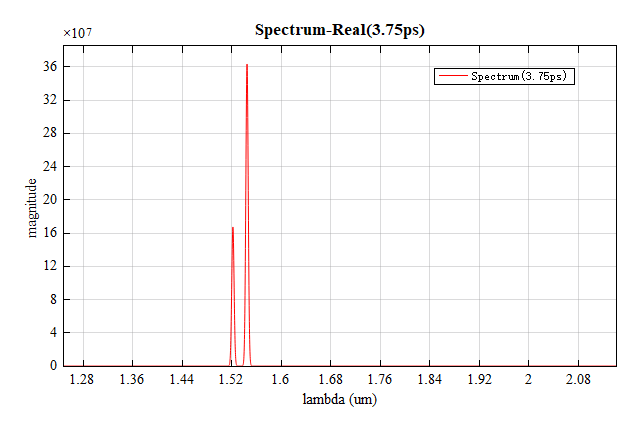
参数分析 #

从上面光谱中的两个共振峰的波长，可以计算得到带隙的大小（带宽）。进一步的，我们可以利用带隙的大小来分析光栅的性能。光栅与光栅中光学模式的相互作用，通常由耦合系数 $\kappa$ 来描述，表达式如下:

$$\kappa=\pi n_g\Delta\lambda/\lambda_0^2$$

其中 $\kappa$为光栅的耦合系数， $\Delta\lambda$ 为带宽， $\lambda_0$为中心波长， $n_g$为中心波长处的群折射率。

刻痕深度对光栅性能的影响 #

设置 $\Delta w$ 从 $0.01\mu m$ 增长到 $0.05\mu m$ 进行扫描，可以观察到光栅刻痕的深度对光栅性能（耦合系数 $\kappa$ ）的影响。打开本案例附录工程，运行参数扫描后，将扫描结果当中的 $\kappa$绘制成散点图，即可得到光栅性能随光栅刻痕深度的变化趋势，如下图所示，与参考文献^[1]Figure7 十分接近。

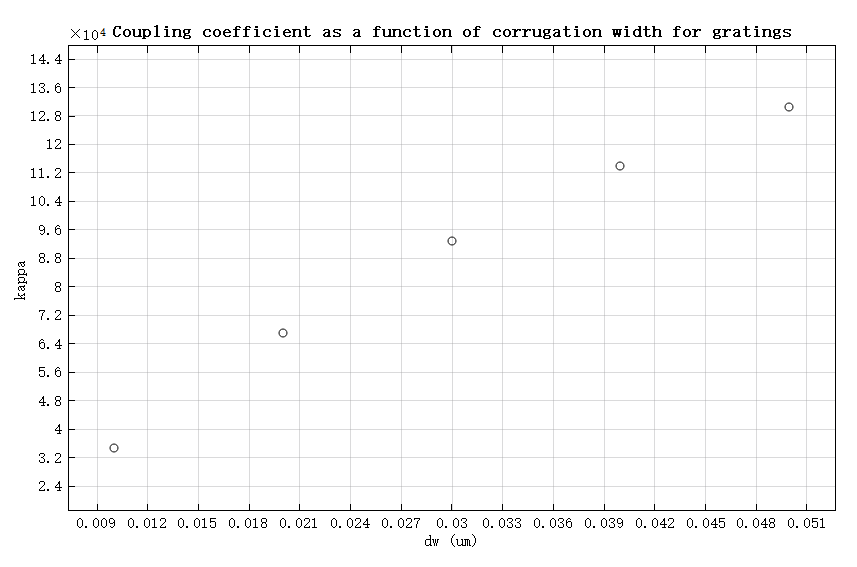
参考文献 #

---

1. X. Wang, et al., "Precise control of the coupling coefficient through destructive interference in silicon waveguide Bragg gratings", Opt. Lett. 39, 5519-5522 (2014). ↩︎