Preface #

In FDTD simulations, there are two main approaches to obtain the far-field distribution of a device. The first is to directly enlarge the simulation domain so that light propagates to the target plane; although straightforward, this approach is computationally expensive. The second is the near-to-far field (NTFF) transformation, which does not require expanding the simulation domain and is suitable for quickly estimating far-field behavior. However, for periodic structures (such as gratings), conventional NTFF methods have limitations in handling the propagation and interference of multiple diffraction orders. To address this, the grating projection(GP) method can be employed, which decomposes the near-field information of the device into plane waves in different directions, thereby accurately reconstructing the field distribution at arbitrary far-field locations in a homogeneous medium. This case demonstrates how GP can be used to efficiently calculate the field distribution in a specified far-field region and validates the reliability of the method by comparison with standard FDTD results.

Simulation settings #

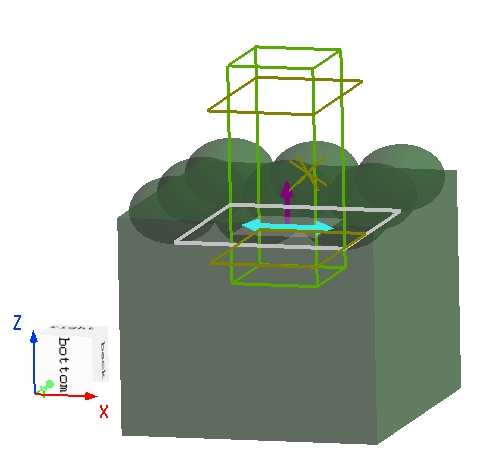
Device introduction #

The model used in this case consists of a glass substrate covered by a gold film, with a circular hole of radius $r=0.2 \mu m$ etched at the center of the film. The structure is periodic in both the $X$ and $Y$ directions, with a period of $1.5 \mu m$. A plane wave source with a wavelength range of $0.4-0.6\ \mu m$ is normally incident from the glass substrate along the $Z$ axis, with the electric field polarized along the $X$ axis. Based on the symmetry of the source and structure, Anti-Symmetric and Symmetric boundary conditions are applied in the $X$ and $Y$ directions, respectively, reducing the simulation domain to one quarter of its original size. When using symmetric/anti-symmetric boundaries for periodic structures, the maximum and minimum boundaries in the corresponding directions should be set to the same type.

Simulation results #

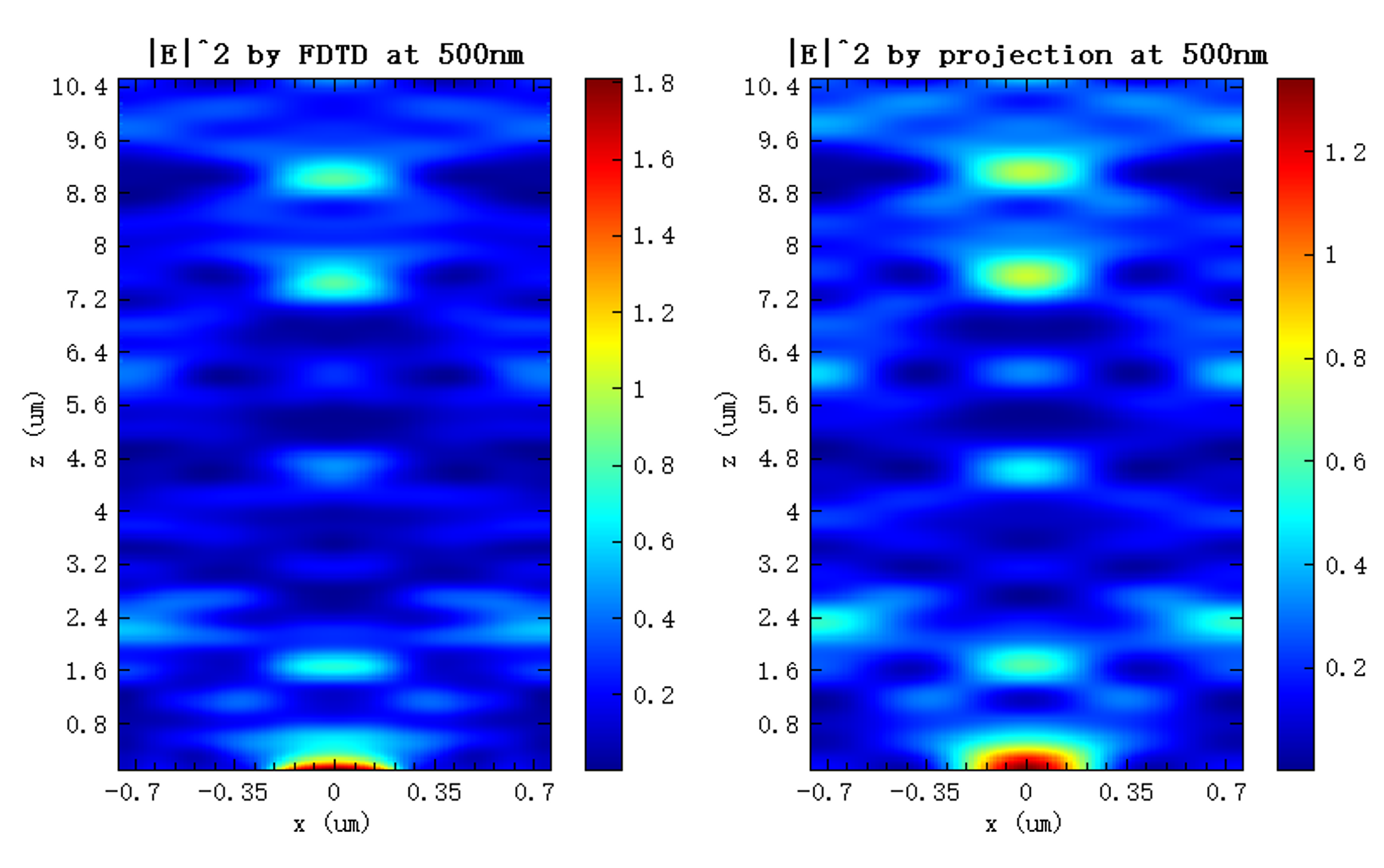
By running the attached solvers_propagate_periodic.msf script, the grating series of script functions are used to perform GP. The electric field recorded by the FDFP monitor at $0.12\ \mu m$ above the structure is decomposed into a set of plane waves, which are then projected onto the target plane according to their wavevector relations to obtain the field distribution at that location. The figure below shows the propagated field intensity distribution at a wavelength of $500\ nm$ on the plane $Y=0$, evaluated $10.5\ \mu m$ above the structure. The left panel corresponds to the result obtained directly from the FDFP monitor, while the right panel shows the result computed using GP.

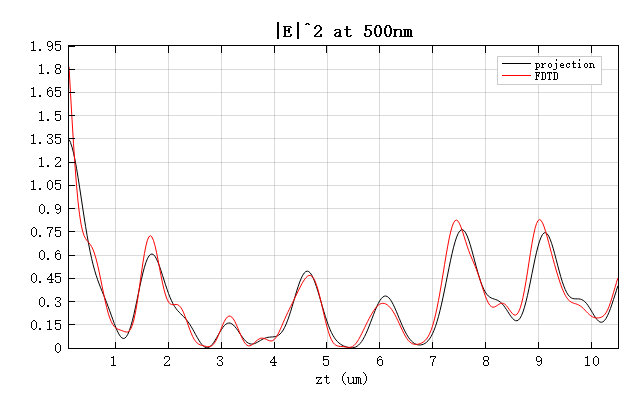
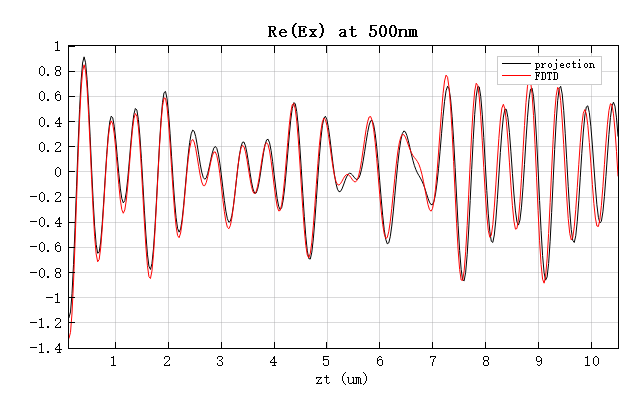
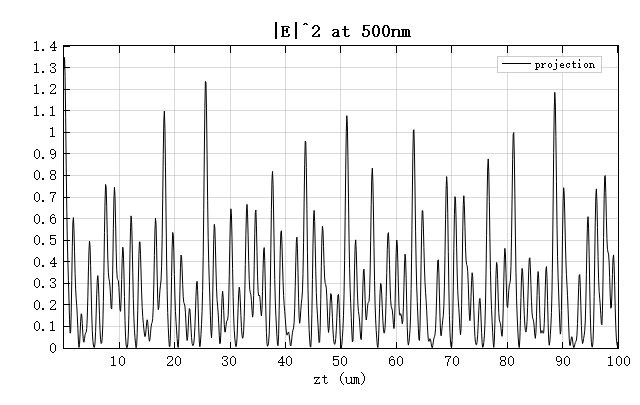
The figure below shows a comparison of the field intensity and the $E_x$ component along $(x,y)=(0,0)$. It can be seen that the projection results are in good agreement with those obtained from the FDTD simulation.

It is worth noting that the GP method is also applicable to oblique incidence. The figure below shows the electric field distribution for an incident angle of $10\degree$ computed using this method. When performing simulations under oblique incidence, the boundary conditions in the $X$ and $Y$ directions should be set to bloch.

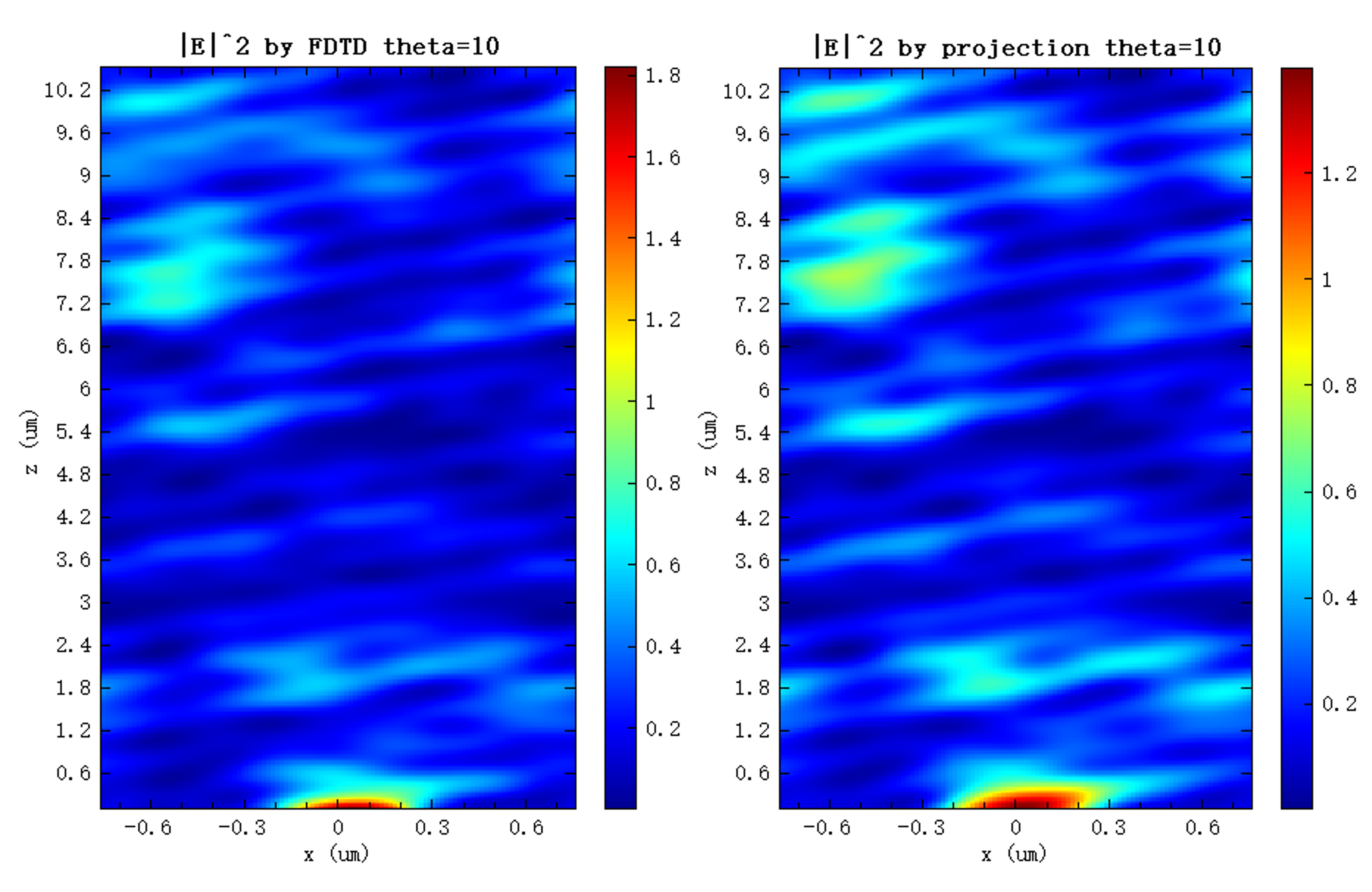
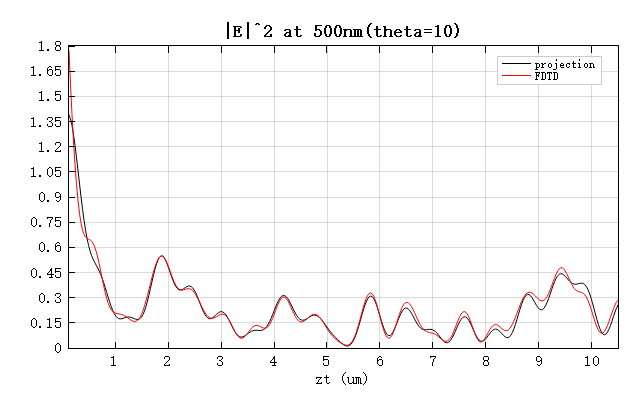
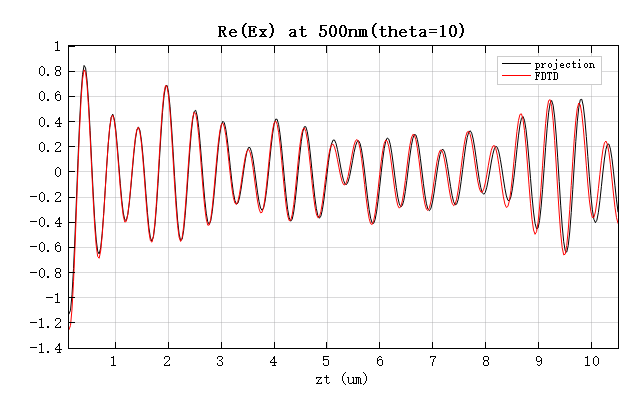
As shown, even for oblique incidence, the GP results are in good agreement with the FDTD simulations. However, the discrepancy between the two increases with propagation distance. This is due to the grid dispersion effect in FDTD simulations: the speed of light on the grid slightly deviates from that in free space and exhibits anisotropy. Therefore, for long-distance propagation, the projection results are actually more accurate.

The figure below shows the optical field at a wavelength of $500\ nm$, obtained using the projection method, after propagating a distance of $100\ \mu m$. You can set test to 0 in the solvers_propagate_periodic.msf script and rerun it to reproduce this result.

Appendixes #

Grating Projection #

Grating projection is an efficient numerical method based on angular spectrum theory and the Floquet–Bloch theorem, specifically designed to handle optical field propagation in periodic structures. This method decomposes the near-field distribution recorded by the monitor into a series of discrete diffracted plane waves according to the grating equation. By computing the propagation of these plane waves in a homogeneous medium, the field distribution at any specified location can be accurately reconstructed.

Basic Principle #

For two-dimensional periodic structures, the diffraction wave vectors satisfy the grating equation:

$k_{x}^{n}=k_{x}^{in}+n\frac{2\pi}{ax}$

$k_{y}^{m}=k_{x}^{in}+m\frac{2\pi}{ay}$

Here, $k_{x}^{n}$ and $k_{y}^{m}$ are the in-plane wave vectors corresponding to the $(n,m)$-th diffraction order, while $ax$ and $ay$ are the periods along the $x$ and $y$ directions, respectively. $k_{x}^{in}$ and $k_{y}^{in}$ are the components of the incident wave vector.

Given the near-field distribution $E(x, y, z_0)$, it can be decomposed as a superposition of plane waves:

$E(x,y,z_0)=\sum_{n,m} E(n,m)exp(i(k_{x}^{n}x+k_{y}^{m}y))$

where the coefficient $E(n,m)$ represents the complex amplitude of the $(n,m)$-th diffracted plane wave, which can be calculated using the gratingvector function.

Field Distribution at Arbitrary Locations #

In a homogeneous medium, the field distribution at any position $z = z_0 + \Delta z$ can be obtained by propagating these plane waves as follows:

$E(x,y,z_0)=\sum_{n,m} E(n,m)exp(i(k_{x}^{n}x+k_{y}^my+k_{z}^{(n,m)}\Delta z))$

where $k_{z}^{(n,m)}$ is the longitudinal wave vector component of the $(n,m)$-th diffraction order:

$k_z^{(n,m)}=\sqrt{k^2-(k_x^n)^2-(k_y^m)^2}$

Here, $k_0$ is the free-space wavenumber. For propagating modes (real $k_z$), the expression describes phase accumulation; for evanescent modes (imaginary $k_z$), it characterizes exponential decay.