Preface #

In nonlinear optics, Four-Wave Mixing (FWM) is a typical third-order nonlinear effect that has been widely applied in all-optical signal processing, wavelength conversion, and the generation of new light sources. When light propagates through a material with Kerr nonlinearity, the nonlinear interaction of multi-frequency optical fields can generate new frequency components, achieving frequency mixing and energy transfer. The Finite-Difference Time-Domain (FDTD) method is capable of directly solving Maxwell's equations incorporating nonlinear terms in the time domain, fully capturing the evolution of the electric field in nonlinear media. Thus, it serves as an effective tool for studying four-wave mixing. This case demonstrates an FDTD simulation workflow for four-wave mixing based on a third-order nonlinear material.

Simulation settings #

Device introduction #

In this case, some simulation settings specific to nonlinear analysis - such as override bandwidth for mesh generation, source intensity, and pulse parameters - are similar to those used in the case Harmonic Generation with Nonlinear Materials and are therefore not be repeated here. The complete model configuration can be found in the project file four_wave.mpps. In this case, three plane wave sources are defined with frequencies of $100\ \text{THz}$, $120\ \text{THz}$, and $140\ \text{THz}$, which are simultaneously incident on the nonlinear slab. By disabling certain sources, you can also observe the simulation results under single-source or multi-source excitation.

Material #

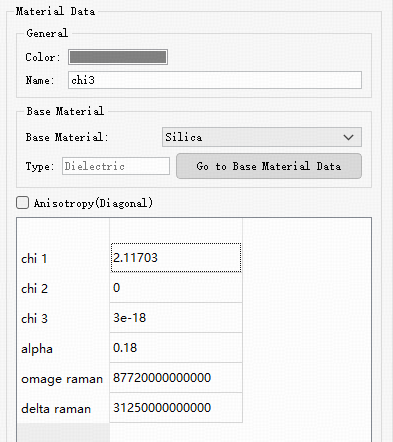
In this case, the material is defined as a third-order nonlinear medium with silica as the base material. For silica fibers, typical parameters are shown in the figure below: $chi1$, $chi2$, and $chi3$ correspond to the first-, second-, and third-order nonlinear polarization coefficients, respectively; $alpha$ denotes the fraction of the Kerr effect in the total nonlinear response (Kerr + Raman scattering); $omega \space raman$ represents the Raman resonance angular frequency; and $delta \space raman$ corresponds to the resonance linewidth.

Simulation results #

Single-Source Excitation #

When only one source is enabled, the optical field passing through the nonlinear slab excites third-harmonic components. The following figures show the output spectra for incident frequencies of $100\ THz$, $120\ THz$, and $140\ THz$, respectively:

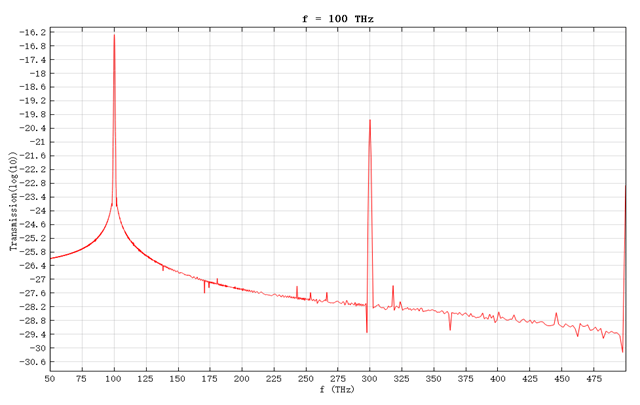
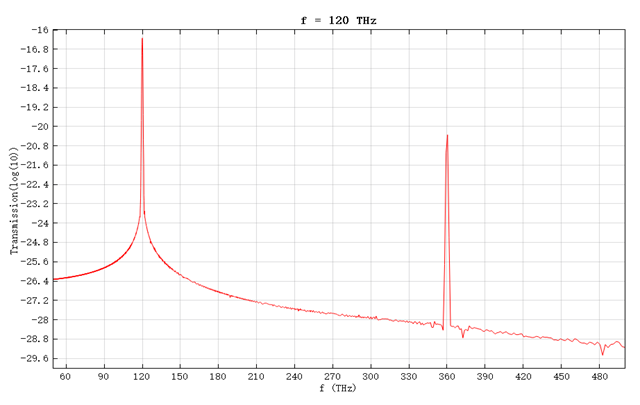
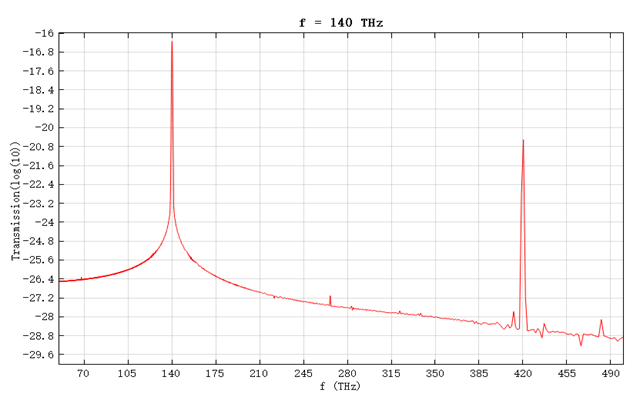
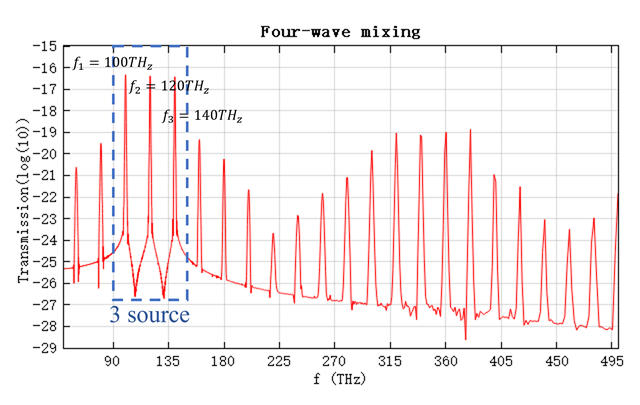
Four-Wave Mixing #

When all three sources are incident simultaneously, the interaction among different frequencies excites new frequency components. In the output spectrum, this appears as a series of additional peaks, which is the manifestation of the four-wave mixing effect: