Preface

In 2D photonic crystals, different lattice types possess completely different band structures. The base settings in FDTD simulations vary with the different lattice types. In this case, a 2D triangular-lattice photonic crystal formed by air cylinders arranged in parallel in the medium is constructed, and its bandstructure is calculated. Based on the following example, some special settings and precautions for FDTD simulation of non-rectangular lattice photonic crystals are introduced.

Simulation settings

Device introduction

The FDTD solver is used to analyze the bandstructure of a triangular-lattice photonic crystal consisting of periodically arranged air cylinders in a homogeneous medium. Similar to the 2D square-lattice photonic crystal, the periodic arrangement of air cylinders in homogeneous media also realizes the periodic refractive index distribution, forming a photonic bandgap, which prevents some specific frequencies of light from entering the structure. In this photonic crystal, the refractive index of the dielectric material is 2, the radius $r$ of the periodically arranged air cylinder is 200 nm, and the lattice spacing $a$ of the triangular-lattice is 500 nm. For such triangular-lattice photonic crystals with non-rectangular lattice structure, at least two lattice cells are required in the FDTD simulation region.

Device construction

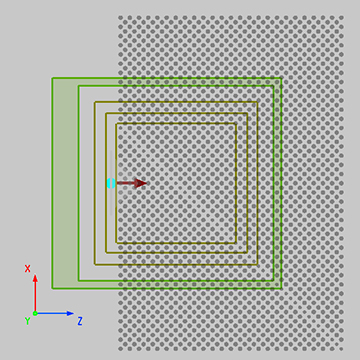
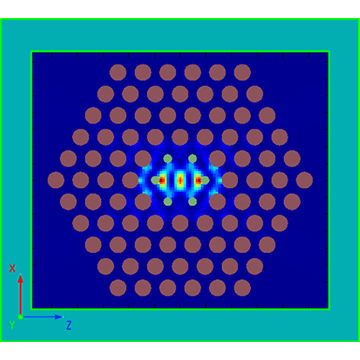
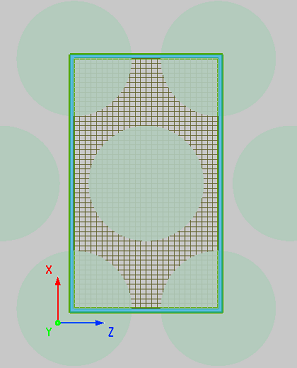
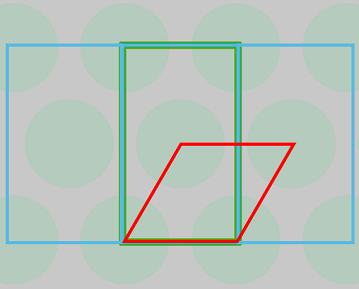
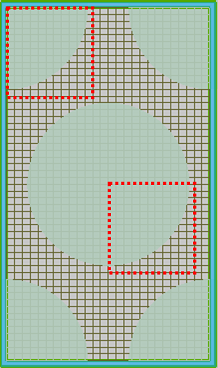
The simulation setup of this case is similar to the case of Bandstructure of 2D Square Lattice, and will not be repeated here. Please download the attached file for detailed information. Because the shape of the FDTD simulation region is limited by the rectangular mesh, the non-rectangular lattice structure can not be simulated with only one complete lattice periodic cell like the rectangular lattice structure. For photonic crystals with 2D triangular lattice or other non-rectangular lattice, the overall lattice structure can only be divided into rectangular regions suitable for FDTD solver. As shown in the figure below, the triangular lattice structure can be seen as a square lattice repeatedly arranged by the rectangular structure inside the green wireframe. Therefore, the simulation region is selected to be consistent with the wireframe, and the structure in it is simulated.

It should be noted that each unit of photonic crystal structure must be partitioned in the same method and size. Ensure the uniformity and periodicity of the refractive index distribution, so as to avoid inaccurate calculation results. As shown in the following figure (within the dotted box), the mesh distributions at the corresponding positions of different structural elements are compared. It is obvious that each circular structure region is partitioned in the same way. This requires that the number of grids in the simulation area must be even, and the grid is symmetrically distributed about the center coordinate axis of the simulation area (On the solver Advanced Settings page, select the 'force symmetric X/Z mesh' option under 'Mesh Generation' to force the construction of a mesh that is symmetric about the X/Z axis.).

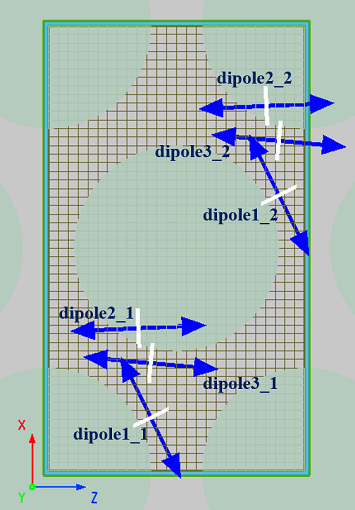
For the model with multiple unit cells in the simulation region, in order to avoid the artificial region folding, we must have a matching dipole source in each unit cell, and each set of matched dipole sources must have exactly the same position in the unit cell. The phase difference $\Delta\phi$ between the dipole sources must satisfy the formula $\Delta\phi = \vec{k} \cdot \Delta \vec{r}$ , where $\vec{k}$ is the wave vector of the simulation and $\Delta \vec{r}$ is the position-varying vector of the two dipole sources. The built-in script of the analysis group 'Dipole Clouds' will complete the construction of such a dipole array by simply setting the variable values in the analysis group according to the photonic crystal. As shown in the figure, three sets of matching dipole sources are constructed.

Simulation results

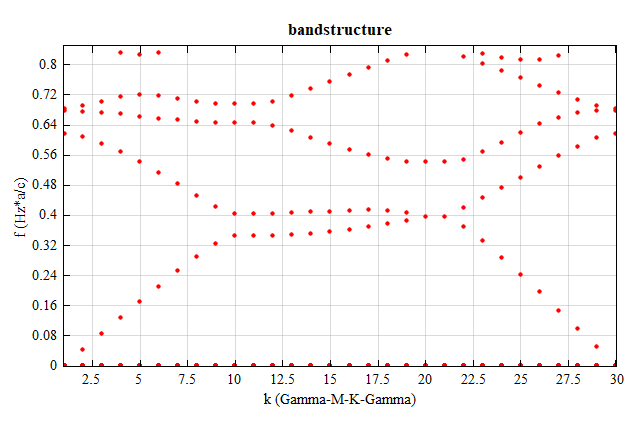
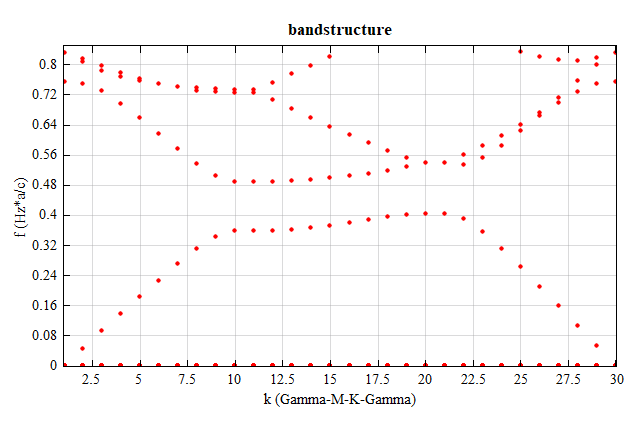
Download and open the attached file triangular_2D.mpps. After running all parameter sweeps, run the script file (triangular_2D.msf) to obtain the sweep results and draw the bandstructure diagram in TE mode, as shown below.

The bandstructure in TM mode can be calculated by changing the polarization type in the solver properties, as shown below.

Recommend

Photonic Crystal Optical Switch Using Line Defects

The self-collimation(SC) effect of photonic crystals(PCs) achieves collimated radiation with almost no diffraction effect when the incident light propagates along a particular direction of the crystal. Line defects in 2D PCs cause bending and splitting of the SC beam. In this example, the effect of "optical switching" can be achieved by altering the line defects (radius of the dielectric rod) in the photonic crystal.

Bandstructure of 2D Square Lattice

Photonic crystals, as a dielectric structure with periodic changes in dielectric constant, can prevent light of a specific frequency from propagating internally, forming a photonic band gap.

Bandstructure of 3D Cubic Lattice

3D Cubic Lattice is a special case of 3D Rectangular Lattice. The lattice spacing of this type of photonic crystal is equal in three axes in space.

Bandstructure of BCC Lattice and FCC Lattice

In this case, BCC and FCC photonic crystals are constructed and their bandstructures are analyzed using FDTD solvers.

Bandstructure of a Magneto-Optical Waveguide

In this case, the optical waveguide model with periodic structure in the propagation axis is constructed, and the bandstructure of the waveguide is analyzed.

Correcting Field Amplitudes for High-Q Cavities

Generally, in the simulation of high-Q resonant cavities, the field amplitude obtained is inaccurate. The reason is that the loss rate in the high-Q resonant cavity is slow. If the simulation time is not long enough, the field in the cavity will not decay to 0 at the end of the simulation. At this time, the amplitude of the mode field in the cavity needs to be corrected to obtain the final actual amplitude. This case constructs a photonic crystal resonant cavity structure to demonstrate how to correct the field amplitude when the simulation time of a high-Q resonant cavity is insufficient.

2D-Periodic Metallic Photonic Crystal Slabs

The ability to modify an object's thermal radiation profile is important in many areas of applied physics and engineering. It has been noted that periodic engineering of devices made of metallic and dielectric materials at the subwavelength scale can change the thermal radiation properties of the device. This case studies the thermal radiation of a photonic crystal obtained by periodically arranging a device made of metallic tungsten and a dielectric material.

Organic Solar Cell with PC Structure

How to improve Organic solar cells'(OSCs) photoelectric conversion efficiency (PCE) is an urgent problem to be solved. One of the more commonly used methods is to add micro-nano structures for light trapping into the photoactive layer of OSCs to increase light absorption, thereby improving PCE. The photonic crystal (PC) structure is used in the photoactive layer of OSCs, which can enhance the light absorption of solar cells in specific wavelength bands. This case uses FDTD simulation to analyze the light absorption of an OSC with a 2D hexagonal-lattice PC structure.

Exciting the Surface Plasmon-Polaritons in Graphene

The chemical potential of graphene can be regulated by methods such as voltage or chemical doping. This property makes graphene highly versatile in the field of material-light interactions, particularly in relation to surface plasmon polaritons (SPPs). By exciting surface plasmons, graphene significantly enhances its ability to interact with light.

Bandstructure of Woodpile Lattice

In this case, the Woodpile-Lattice photonic crystal is constructed, and the FDTD solver is used to explore the energy bandstructure of the photonic crystal.