2D正方晶格能带结构
前言
光子晶体(Photonics Crystal,PC)是一种介电常数周期性变化的电介质结构,可以阻止特定频率的光在 PC 中传播,形成光子带隙[1]。本案例构建 2D 正方晶格 PC 模型,使用 FDTD 分析其能带结构。通过本案例详细介绍了使用本软件在对 PC 能带结构进行 FDTD 仿真计算时的一些特殊设置及注意事项。
仿真设置
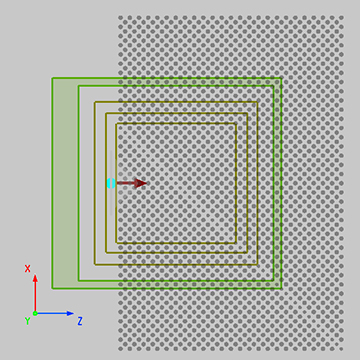
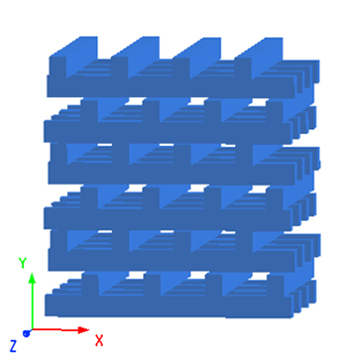
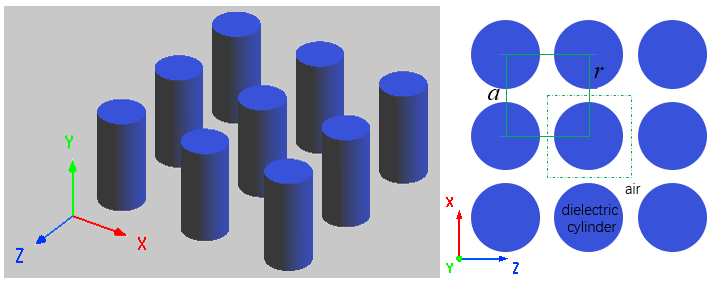
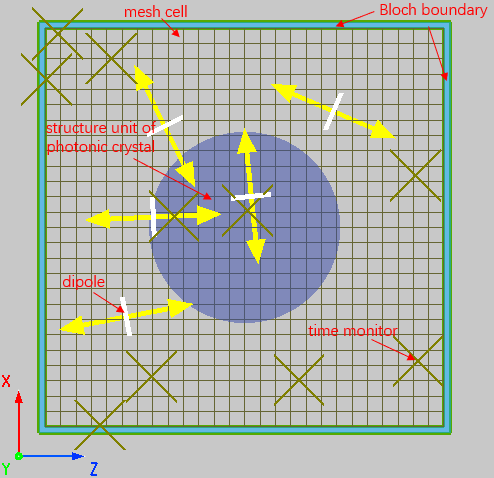
本案例使用 FDTD 分析由均匀介质圆柱周期排列组成的正方晶格光子晶体的能带结构。如图所示,半径为 的均匀介质圆柱体,以晶格间距 在空气中沿着 z 和 x 轴周期性排列,形成 2D 正方晶格光子晶体。2D 正方晶格结构在 zx 平面内周期性变化,结构单元在 y 轴向无限延伸,所以在本案例中使用 2D FDTD 建模仿真,将仿真区域设置为 2D 平面进行计算。对于这种周期结构,在 FDTD 中使用周期性边界条件,此仿真只需要其中一个晶格结构单元,如下图中虚线框所示。
模型构建
光子晶体结构模型
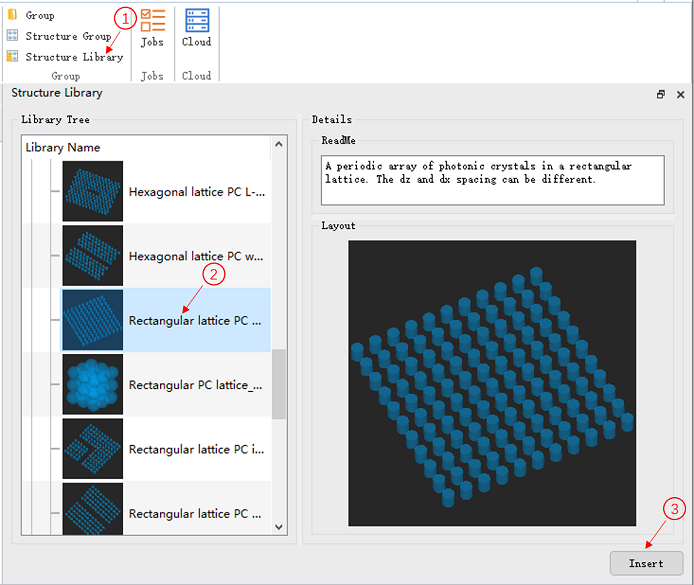
光子晶体中不同的折射率分布拥有不同的能带结构,决定光子晶体能带结构的主要因素是内部介质的折射率与结构的周期常数[2]。对于本模型,介质材料的折射率为 2.00,背景介质为空气,周期性排列的介质圆柱的半径r为 0.12 μm,构成方晶格的晶格间距a为 0.5 μm。对于圆柱的高度,2D FDTD 中此参数可以不做考虑,默认设置为 0.5 μm。软件内置的结构组库中包含一些常见的光子晶体结构模型,本案例中可以直接选择其中的Rectangular lattice PC array结构组进行添加,并根据模型参数修改对应的脚本变量即可。
求解器设置
Bloch 边界条件
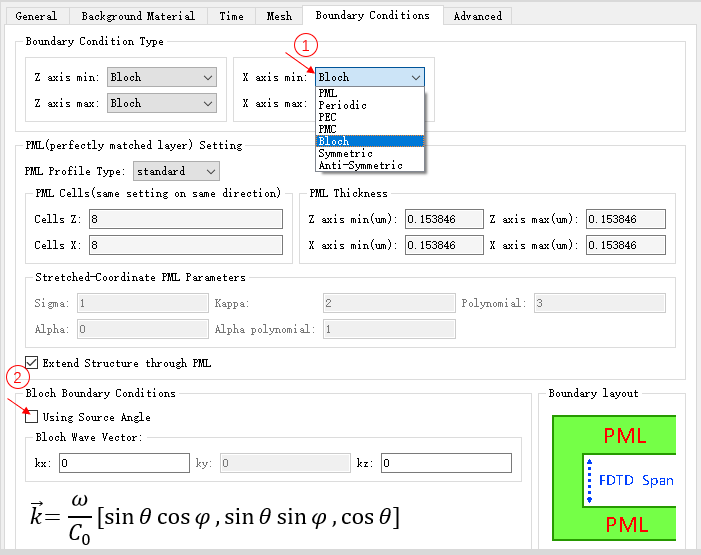
本案例中光子晶体由介质圆柱在 2D 空间中按正方晶格周期性排列而成,可以仅对周期单晶格进行建模仿真。为了使模型保持周期性阵列结构,在仿真区域的 z 与 x 轴向的边界使用 Bloch 周期性边界条件。在使用 Bloch 边界条件的情况下,需要设置 Bloch 波矢。在不同的波矢 下,光子晶体中能稳定存在的模式不同[3]。根据晶格的布里渊区,来对 Bloch 波矢进行自定义。用户可以勾选 Using Source Angle,软件将会自动根据光源角度设置 Bloch 波矢。本案例中需要进行目标波矢的扫描,所以采取自定义波矢的形式。
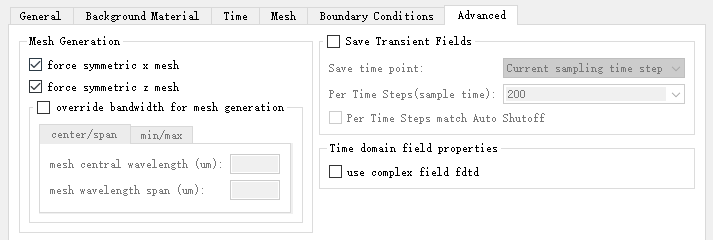
强制网格对称
对于光子晶体仿真,在网格剖分的时候,要保证每个结构单元的网格剖分方式及尺寸完全一致,确保折射率分布的统一性和周期性,以免造成计算结果不准确的现象。在高级设置页面,可以勾选 Mesh Generation 中的 force symmetric x/z mesh 选项,强制构建的网格关于 X/Z 轴对称,确保生成的折射率数据完全符合光子晶体周期条件。
光源及监视器
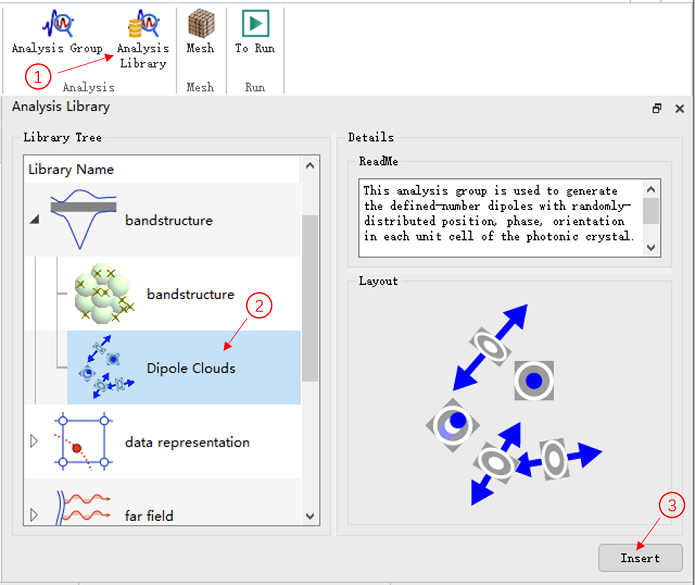
分析组:Dipole Clouds
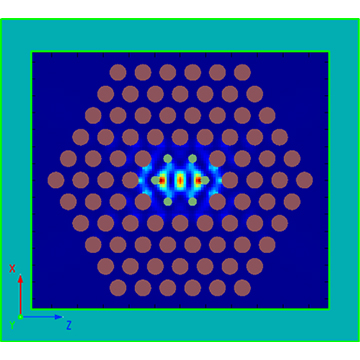
对于 FDTD 仿真,需要添加合适的光源,作为输入模式信号。为了尽可能地激发出光子晶体中可以稳定存在的所有模式,在仿真区域中随机放置多个随机方向的宽带偶极子源。通过在仿真组件中添加软件内置分析组 Dipole Clouds 来对这种偶极子阵列进行构建。使用分析组 Dipole Clouds 构建随机偶极子源时,需要根据光子晶体的晶格类型设置脚本变量值,用来确定偶极子源阵列的分布区域及个数。对于不同的晶格类型和仿真维度,需要设置的变量不同。(详细介绍见分析组设置页面。)
分析组:bandstructure
软件内置分析组 bandstructure 在软件内的添加方式与分析组 Dipole Clouds 相同。在计算特定波矢下模型频谱的过程中,需要使用 time monitor 收集由偶极子源阵列激发出的场时间信号,通过在目标区域内构建多个随机位置的 time monitor 确保模式信号的完全收集。分析组 Analysis - Script 页面中的脚本会将每一个 time monitor 收集到的场时间信号进行傅里叶变换并汇总,最终得到目标频谱(Spectrum)。需要注意的是,根据傅里叶变换原理,为了得到更准确的频域结果,FDTD 就必须有足够的仿真时间。同时仿真刚开始存在的干扰模式信号也会充分衰减,最终分析组会获得稳定存在于光子晶体中的模式信号。
包含所有组件的模型的平面图如下所示,详见附件中的工程文件(square2D.mpps)。接下来可以进行仿真,得到目标结果,并进行数据后处理。
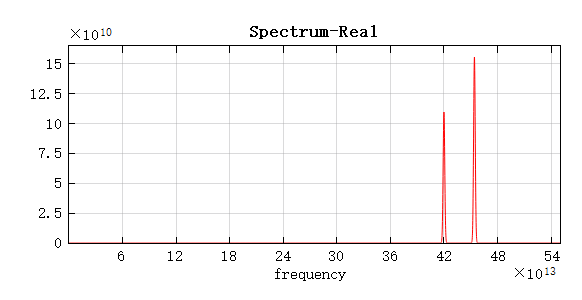
仿真结果
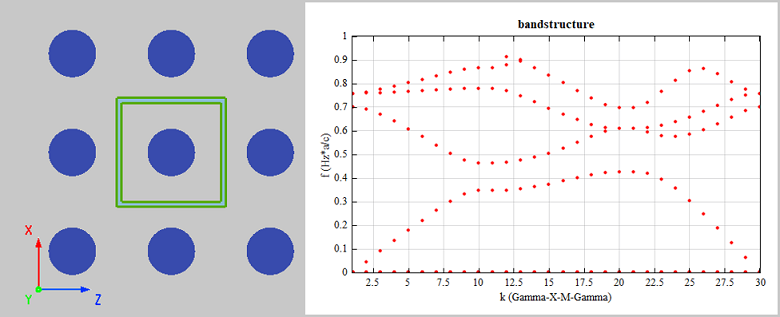
仿真完成后,查看分析组计算结果,可以得到特定波矢下的频谱。如下图所示,当 Bloch 波矢分量均为 0 时,频谱图中存在两个共振峰,这说明此 Bloch 波矢下光子晶体中可以稳定存在两个模式。
对于 2D 正方晶格,光波仅在 zx 平面内进行传播,在平面外的波矢分量 ky 等于 0。不可约的布里渊区域为如下图所示的三角形 Γ-X-M,通过调节波矢分量 kz 与 kx,获得沿着三角形的边缘方向,从中心 Γ 到 X,再到 M,最后回到中心 Γ 的波矢。计算能带结构需要得到每个目标波矢下可稳定存在的所有模式,所以必须要使用参数扫描来计算每一个波矢下的频谱。
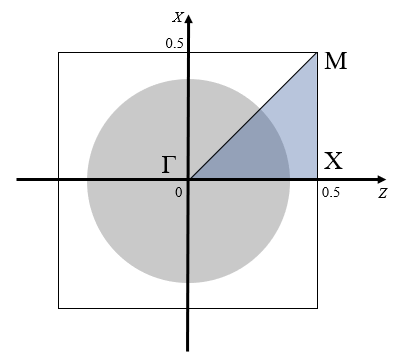
参数分析
本案例中,需针对不同的 Bloch 波矢(bloch kz,bloch kx)进行参数扫描。能带结构图中的波矢为归一化波矢,而在 FDTD 求解器计算时使用 Bloch 波矢,所以需要进行转换。归一化波矢范围由布里渊区特殊点坐标值决定,并且 ,所以由归一化波矢范围可计算对应的 Bloch 波矢参数扫描范围。本案例中需要计算每个波矢下的频谱,以获得每个波矢下可以稳定存在的模式,所以选择分析组 bandstructure 的结果 Spectrum 作为本次扫描的输出对象。
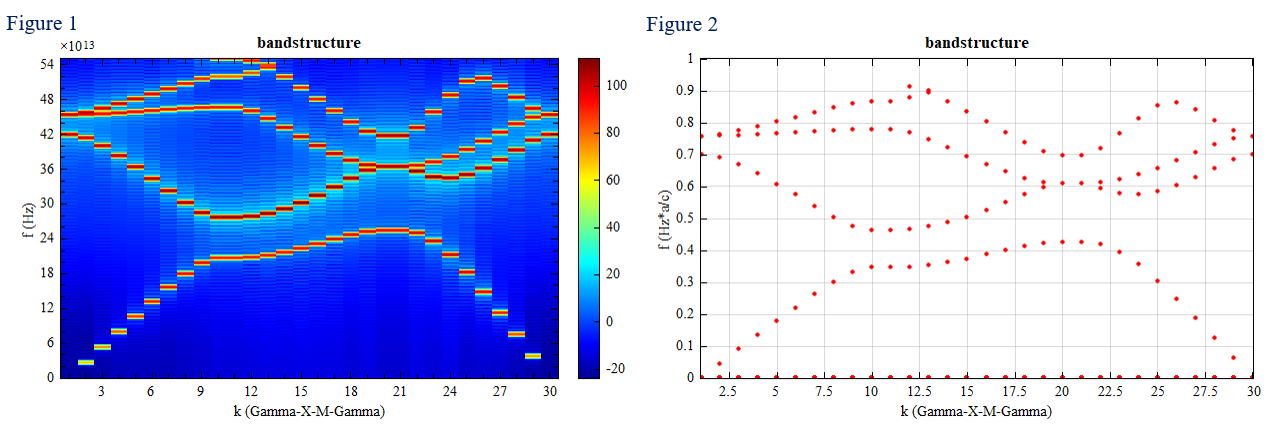
所有的参数扫描运行完成后,打开本光子晶体案例对应的能带结构计算脚本文件(square2D.msf)并运行。软件在脚本运行完成后自动显示计算的结果,如下图中的 Figure 1 和 Figure 2 所示。Figure 1 由波矢、频率和对应频谱数据绘制而成,图中的横坐标代表从布里渊区中心 Γ 到 X,再到 M,最后回到中心 Γ 的波矢,轴上的 30 个坐标点为按参数扫描顺序排列的归一化波矢数值点,纵坐标代表频率值,图中 colorbar 颜色代表每个波矢下频谱中各频率的信号幅度大小。从 Figure 1 中的颜色分布大概可以看出光子晶体的能带结构。最终的能带结构图如 Figure 2 所示,由波矢及其对应的归一化共振频率( )数据绘制而成,图中横坐标代表归一化波矢,纵坐标代表归一化频率,而图中的点代表对应波矢下可以稳定存在的模式。
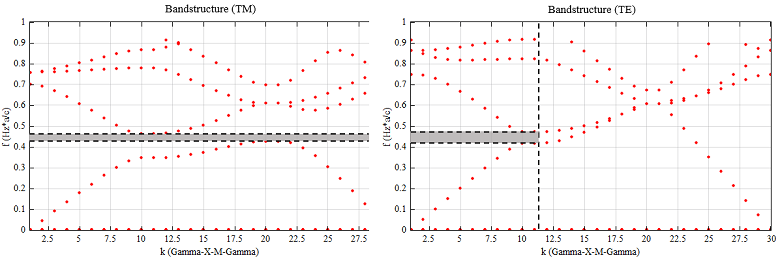
2D 光子晶体为介质在平面内的周期性分布,光波在此平面内传播时,可以看作是两种独立的偏振模式,每种偏振模式拥有自己的能带结构。在 2D FDTD 中,可以通过改变求解器属性中的偏振类型分别求解 TM 和 TE 模式下的能带结构。最终根据能带结构图可以得出 2D 正方晶格光子晶体的能带结构,其中 TM/TE 模式下对应的禁带范围如下图中曲线中间的阴影区域所示。
参考文献
Joannopoulos J D , Villeneuve P R , Fan S . Photonic crystals: putting a new twist on light[J]. Nature, 1997, 386(6621):143-149. ↩︎
Joannopoulos J D , Johnson S G , Winn J N . Photonic crystals:molding the flow of light[M]. Princeton University Press, 1995. ↩︎
Kittel C . Introduction to Solid State Physics, 7th ed[M]. John Wiley & Sons, New York, 1996. ↩︎