Preface #

In recent years, inverse design has become an important methodology in the development of photonic devices. Compared to the traditional forward design process, which relies heavily on experience, intuition, or extensive parameter sweeps, inverse design reframes device development as an optimization problem with well-defined performance objectives. By specifying the desired electromagnetic response and allowing algorithms to freely explore the design space, inverse design can automatically generate high‑performance photonic structures that are often difficult to derive from human experience alone.

In the case Inverse Design of Y Branch, we demonstrated a parametric inverse design method for a 2D Y‑branch splitter, achieving significant performance improvement by automatically optimizing a small number of geometric control parameters. However, the parametric design approach inherently requires predefined assumptions about the structural form, which limits its design freedom to some extent.

In this case, we further introduce the Topology Optimization method for the design of a 2D Y‑branch splitter. This method makes no prior assumptions about the device geometry and instead directly optimizes the material distribution within the design region, thereby significantly expanding the design freedom. Through this case, we demonstrate the powerful capability of topology‑based inverse design in both structural generation and performance optimization of photonic devices.

Simulation settings #

The complete simulation and optimization workflow in this case is driven automatically by the attached Python script splitter_topology_2D_TE.py. The entire process is fully implemented using SimWorks' Python API and optimization framework, eliminating the need for manual structure creation or source configuration within the software's graphical interface.

The overall structure of the script is largely consistent with the previous case study, Inverse Design of Y Branch, and primarily consists of the following core modules:

• Basic Environment Setup
  The script first configures the software interface path and imports the necessary Python dependencies, including the numerical computation library NumPy and SimWorks' Python API.

  import os
  import sys
  
  # This is the default installation path. If you install the software in a different directory, please update the path accordingly.
  os.add_dll_directory(r"C:\Program Files\SimWorks\SimWorks FD Solutions\bin")
  sys.path.append(r"C:\Program Files\SimWorks\SimWorks FD Solutions\api\python")
  
  import numpy as np
  import simworks
  

  Subsequently, the script loads SimWorks modules related to topology optimization, including topology geometry description, objective function definition, and optimizer interfaces. Together, these modules form a complete automated inverse design framework.

• Topology Geometry Modeling

  Unlike the parametric geometry method using "control points + spline interpolation" in the case Inverse Design of Y Branch, this case adopts a topology optimization strategy based on a pixelated design region.

  A two-dimensional topology optimization region is defined within the splitting area of the device and discretized into a regular grid of pixels. Each pixel corresponds to a continuous design variable, representing the effective dielectric constant at that location. Its value is constrained between the dielectric constants of the cladding material and the waveguide material.

  The topology optimization region is defined using the TopologyOptimization2D class. Its core parameters describe the initial state of the design variables, material constraints, and the spatial discretization method, as detailed below:

  geometry = TopologyOptimization2D(
      params=params,
      eps_min=eps_min,
      eps_max=eps_max,
      x=x_pos,
      y=y_pos,
      z=0,
      filter_R=filter_R
  )
  

  The physical meaning of each parameter is as follows:

  1. Params
     Used to define the initial distribution of design variables for topology optimization. It can serve both as the initial geometric condition and, in multi‑stage optimization, be passed from the results of a previous iteration to continue optimization.

  2. eps_min
     The minimum allowable dielectric constant within the design region, corresponding to the dielectric constant of the cladding material. It defines the physical lower bound for low‑refractive‑index areas.

  3. eps_max
     The maximum allowable dielectric constant within the design region, corresponding to the dielectric constant of the waveguide core material. It defines the physical upper bound for high‑refractive‑index areas.

  4. x, y
     Represent the spatial coordinates of the topology optimization region in the x‑ and y‑directions, respectively. They are used to establish the spatial mapping between design variables and FDTD grid cells, enabling two-dimensional topology modeling.

  5. z
     The position of the topology optimization region in the z‑direction. Since this case involves a two-dimensional topology design, this parameter is fixed at 0.

  6. filter_R
     The radius parameter of the Heaviside filter, used to spatially smooth the design variables. This helps suppress overly small feature sizes and improves the manufacturability and numerical stability of the structure.

  In this case, the pixel size is set to $20\ nm \times 20\ nm$, the optimization region length is approximately $3\ \mu m$, and structural symmetry is leveraged so that only the upper half region is optimized. This topology modeling approach significantly enhances design freedom, enabling the algorithm to autonomously generate high‑performance structures without any predefined geometric assumptions.

  

• Material Parameters and Initial Conditions

  The material parameters for the topology optimization region are set as follows:

  Minimum dielectric constant

  $\epsilon_{min} = 1.44^2\ (SiO_2)$

  Maximum dielectric constant

  $\epsilon_{max} = 2.8^2\ (Equivalent\ Silicon\ Waveguide)$

  Here, $\epsilon_{\max}$ is not the intrinsic dielectric constant of silicon. Instead, it is calculated from the effective refractive index of the fundamental mode in a three‑dimensional silicon waveguide under a given thickness. It represents the equivalent electromagnetic response of the silicon waveguide in the two-dimensional simulation. Therefore, although the topology optimization process is performed on a 2D plane, this modeling approach essentially reflects a quasi‑three‑dimensional simulation approximation.

  To avoid imposing any artificial geometric bias on the final result, the initial condition is set as a uniform intermediate value across the entire design region:

  initial_cond = 0.5 * np.ones((x_points, y_points))
  

  This setup ensures that the optimization process is driven solely by performance objectives, rather than by any initial structural assumptions.

• Optimization Problem Formulation

  Objective Function Definition

  Similar to the previous case, the optimization objective in this case is defined using the Mode Match module. A field monitor is set at the output port to evaluate the mode field matching for the fundamental TE mode along the propagation direction.

  fom = ModeMatch(
      monitor_name='fom',
      mode_number='Fundamental TE mode',
      direction='Forward',
      norm_p=2,
      target_fom=0.5
  )
  

  The objective function reflects the excitation efficiency of the target mode at the output port, corresponding to the desired equal‑power splitting behavior.

  Multi‑Wavelength Optimization Setup

  To improve the device's bandwidth performance in practical applications, the optimization is performed simultaneously across the wavelength band from 1450\ nm to 1650\ nm, with 11 discrete wavelength points selected:

  wavelengths = Wavelengths(start=1450e-9, stop=1650e-9, points=11)
  

  The final optimization objective is the combined performance under these multi‑wavelength conditions.

  Optimization Algorithm and Smoothing Constraint

  The optimizer uses the L‑BFGS‑B quasi‑Newton algorithm, which offers good convergence efficiency for high‑dimensional continuous‑variable optimization problems.

  optimizer = ScipyOptimizers(
      max_iter=50,
      method='L-BFGS-B',
      pgtol=1e-6,
      ftol=1e-4,
      scale_initial_gradient_to=0.25
  )
  

  To ensure manufacturability of the final structure and suppress non‑physical small‑scale features, a spatial smoothing filter is applied to the design variables in each iteration. The filter radius corresponds to a physical scale of approximately 500\ nm, which helps eliminate sharp corners and fine isolated structures.

• Automated Optimization Workflow

  After integrating the modules described above, the script initiates a fully automated closed-loop topology inverse design process. The workflow proceeds as follows:

  1. Update the dielectric constant distribution within the design region based on the current design variables.

  2. Automatically invoke SimWorks to perform electromagnetic simulations.

  3. Calculate the mode field matching at the output port as the objective function value.

  4. Compute the gradient of the objective function with respect to all pixel variables using the adjoint method.

  5. Update the design variables using the optimizer.

  This process continues iteratively until the objective function converges or the maximum number of iterations is reached.

Simulation results #

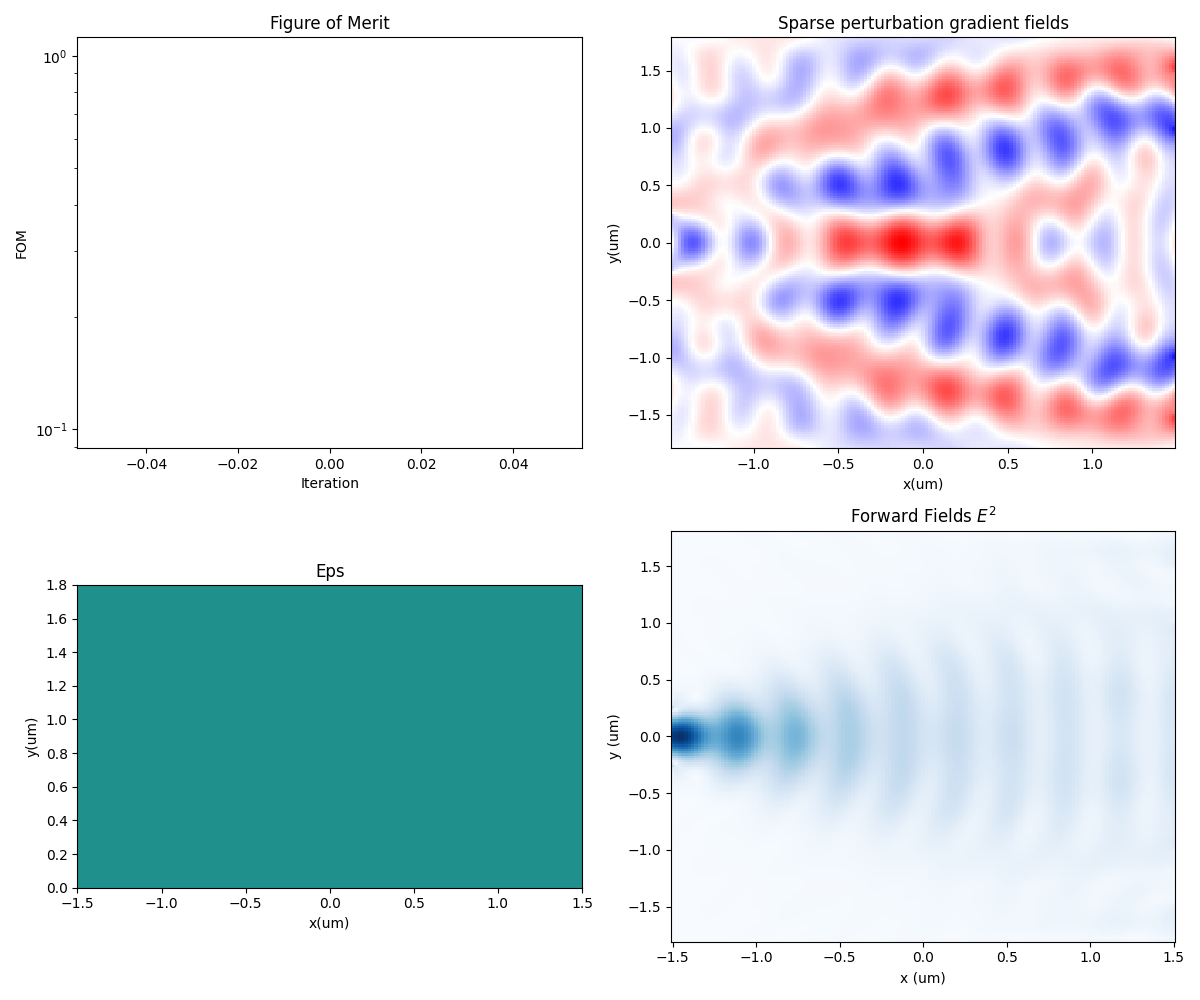
To illustrate the evolution of structural morphology and device performance throughout the topology optimization process, we first present the simulation results from the initial optimization stage. The figure below shows the dielectric constant distribution in the design region under the initial conditions and the corresponding optical field propagation. It can be observed that at this stage, the splitting region is filled with uniform material, lacking any effective energy-guiding structures. As a result, the optical field experiences significant scattering and radiation loss within the splitting region, leading to low overall splitting efficiency.

As the optimization iterations proceed, the algorithm gradually "carves out" a functionally defined dielectric distribution within the design region. The initially continuous and uniform material distribution evolves into distinct energy‑guiding channels, enabling the input optical field to perform the splitting process with significantly higher efficiency.

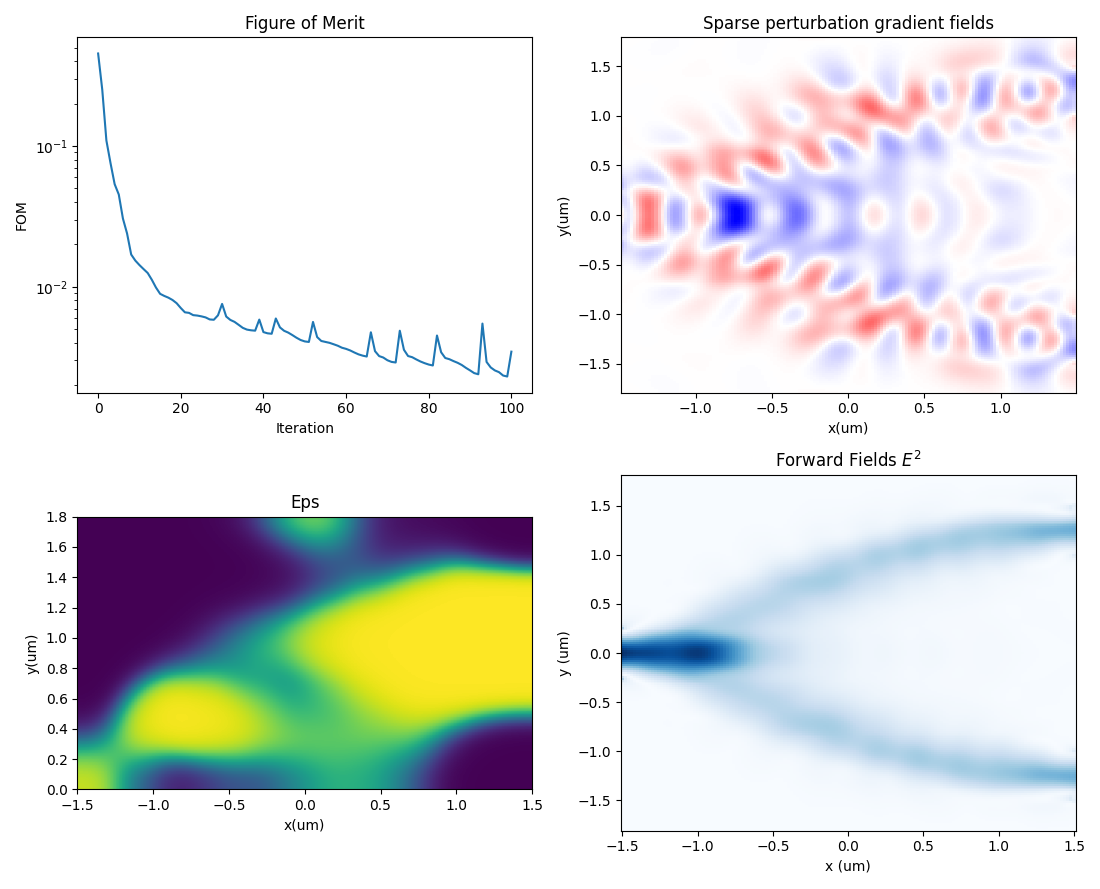
During the topology optimization process, the program automatically saves the current design state after each iteration. Specifically, a corresponding .npz data file is generated for every iteration, recording the topology design variable distribution and the corresponding objective function evaluation result for that iteration.

With these intermediate result files, it is possible to fully reconstruct the evolution trajectory of the dielectric constant distribution in the design region throughout the optimization process and perform post‑processing analysis on the convergence behavior of the objective function. This mechanism provides the topology optimization workflow with strong traceability and reproducibility. Users can not only visualize the optimization path but also filter or further process intermediate structures.

The final topology‑optimized structure is shown in the figure below. It can be directly opened in the SimWorks software for more detailed electromagnetic performance analysis.

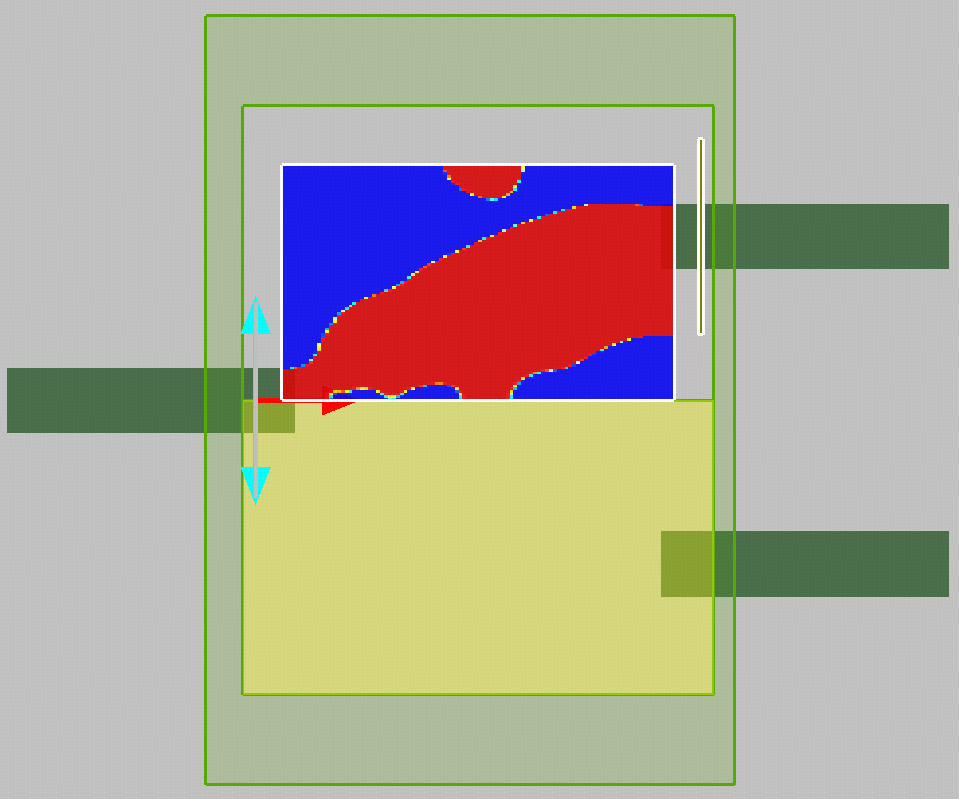
The corresponding final optical field propagation distribution is shown in the figure below. It can be observed that the input optical energy is smoothly and symmetrically guided to the two output ports, while radiation loss within the splitting region is significantly reduced.

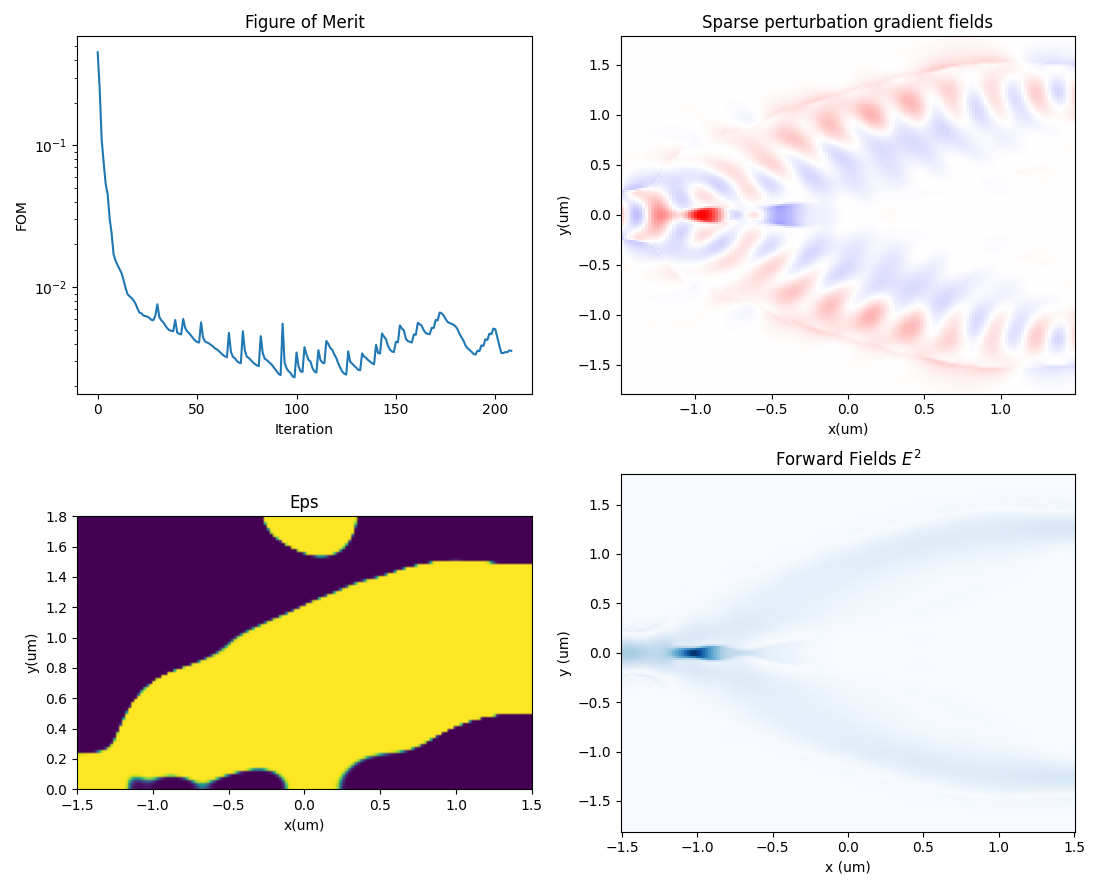
The results indicate that after topology‑based inverse design optimization, the Y‑branch splitter achieves stable equal‑power splitting behavior across the target wavelength range and demonstrates good bandwidth performance within the limited device footprint. This outcome further validates the effectiveness and practical engineering value of the topology optimization method for automatically generating complex photonic devices.