Mesh Setting #

This section describes mesh setting in the solver.

Mesh is one of the most critical settings in a solver, directly impacting simulation accuracy and computational efficiency. Proper mesh partitioning can effectively balance computational resources and simulation accuracy, avoiding numerical errors and resource waste.

Mesh Type #

The mesh type determines the basic partitioning method. SimWorks supports the following three types:

Name	Description	Applicable Scenarios and Recommendations
Uniform	Each mesh cell has the same size.	Suitable for simple structures with smooth variations, enabling quick simulations and debugging. Ideal for most standard simulation scenarios.
Semi-auto nonuniform	Users can customize local mesh sizes to meet specific simulation needs.	Suitable for complex structures where certain regions require higher accuracy. Requires users to have some experience in mesh settings.
Auto nonuniform	Automatically generates nonuniform meshes based on user-defined Accuracy Level to improve simulation accuracy and computational efficiency.	The default mesh type in the software. Recommended for most complex structures, especially multi-scale problems, as it automatically balances accuracy and computational load.

Mesh Accuracy Level #

For Auto nonuniform mesh, the Accuracy level must be set. The mesh accuracy is classified into 10 levels, with level 1 being the coarsest and level 10 being the finest. The expression is:

$N=\cfrac{\lambda_0}{n \Delta}$

where $\lambda_0$ is the wavelength in a vacuum, $n$ is the refractive index of the material, and $\Delta$ is the grid size.
This equation indicates that the mesh partitioning is related to the wavelength and the refractive index of the material. For example, in a vacuum, at accuracy level 1, 6 grids are divided within the spatial extent of a single wavelength; at level 2, there are 10 grids, and so on, increasing by 4 grids per level. In high-refractive-index materials, smaller grids are used. Finer grids reduce the effects of numerical dispersion but significantly increase computational speed and resource requirements. Users are advised to balance specific project needs and computational resources to select an appropriate accuracy level. For most simulations, an accuracy level between 2 and 5 is sufficient.

Mesh Grading Factor #

For Semi-auto nonuniform mesh, users can set the Mesh grading factor to customize the mesh growth rate. This parameter controls the smoothness of mesh size transitions. A smaller factor results in smoother transitions, reducing numerical errors. Users can adjust this parameter based on the complexity of the structure to ensure refined meshes in critical regions with natural transitions. This parameter must be set in conjunction with the mesh definition type, as detailed in the case studies below.

Mesh Refinement #

Mesh refinement is used to improve the accuracy of calculations at material interfaces in simulations, effectively reducing numerical dispersion and errors. Note that mesh refinement does not change the mesh partitioning itself but influences simulation results by calculating the effective permittivity within mesh cells. The main mesh refinement methods include:

• Staircase: When a single mesh cell contains multiple materials, the staircase refinement method fills the entire cell with a single material.
• Conformal: The conformal refinement method calculates the average permittivity of subcells at material boundaries, achieving higher interface resolution. Conformal refinement can yield accurate results even with relatively coarse meshes.

The software currently supports the following mesh refinement methods:

Name	Description	Applicable Scenarios and Recommendations
Staircase	Assigns a single material property to the mesh based on whether the Yee mesh center is within the structure.	Suitable for structures with regular boundaries or simulations where boundary accuracy is not critical.
Conformal variant V-EP	Calculates the effective permittivity by averaging the volumes of different materials within the same mesh.	Suitable for quick conformal mesh construction for non-dispersive materials.
Conformal variant VP-EP 0	Calculates the effective permittivity based on material proportions and the normal direction of the electric field at material boundaries.	The default refinement method in the software, applicable only to non-dispersive materials.
Conformal variant VP-EP 1	An extended algorithm of VP-EP 0 for dispersive materials; supports both dispersive and non-dispersive materials but reduces computational speed due to dispersion current calculations.	Suitable for high-accuracy simulations requiring dispersion effects. Note: Simulations may occasionally diverge when VP-EP 1 materials extend through PML boundary conditions.
Conformal variant Yu Mittra 1	Modifies Maxwell’s equations near conductor surfaces using loop integration, where the internal electric field of an ideal conductor is 0.	Suitable for electromagnetic simulations involving metallic structures, such as antennas and waveguides.
Conformal variant Yu Mittra 2	Calculates the effective permittivity at dielectric or non-metallic material surfaces based on the weighted average of lengths occupied by different materials on the corresponding Yee mesh edge.	Applicable to conformal mesh discretization of dielectric or non-metallic materials

Mesh refinement subcells #

Conformal refinement methods support subdividing a single mesh into multiple subcells to calculate more accurate effective permittivity. More subcells result in higher accuracy but also increase computational load. The default settings are usually sufficient, but users can increase the number of subcells for special high-accuracy requirements.

Name	Default	Description
Mesh refinement subcells	5	Except for Staircase, all other refinement methods include this parameter. It specifies how many subcells a single mesh is divided into for effective permittivity calculations. In 2D simulations, a single mesh is subdivided into $N\times N$ subcells; in 3D simulations, it is subdivided into $N\times N\times N$ subcells, where $N$ is the user-specified value.

Mesh Definition Type #

The Mesh definition type provides finer control over mesh partitioning in each direction. The related settings are displayed when the mesh type is set to Uniform or Semi-auto nonuniform. The available options differ for these two types, as shown below:

Name	Description	Applicable Scenarios and Recommendations
Mesh size	Sets the physical size of mesh cells in each direction (X/Y/Z) within the simulation region.	Available for both Uniform and Semi-auto nonuniform meshes. For Uniform mesh, generates uniform meshes based on the specified size. For Semi-auto nonuniform mesh, combines with custom meshes to generate nonuniform meshes.
Number of mesh cells	Sets the total number of mesh cells in each direction (X/Y/Z) within the simulation region.	Available for both Uniform and Semi-auto nonuniform meshes. Regardless of the mesh type, generates uniform meshes based on the specified number of cells.
Mesh cells per wavelength	Sets the number of mesh cells per unit wavelength (or sampling points per wavelength).	Available only for Semi-auto nonuniform meshes. Commonly used to generate nonuniform meshes for different materials.
Mesh size and Mesh cells per wavelength	Selects the smaller mesh size between Mesh size and Mesh cells per wavelength for partitioning.	Available only for Semi-auto nonuniform meshes.

In Semi-auto nonuniform mesh settings, the Mesh grading factor can further control the rate of mesh size transitions, ensuring smooth transitions and avoiding numerical errors. Note that this option is only effective under specific mesh definition types. For example, it is applicable only when generating nonuniform meshes using the first, third, or fourth options in the table above. Refer to Case Study 2 below for specific usage methods.

Name	Default	Description
Mesh grading factor	1.41421	The maximum growth rate of the mesh. For example, $a=dx(i+1)/dx(i)$, where $a$ should be less than or equal to the grading factor. The grading factor should be between 1 and 2.

Time Step Size #

Time step size:

Name	Default	Description
Stability factor	0.99	The ratio between the maximum allowable step size of each time step and the actual time step size used. This parameter determines if the time step size is small enough to maintain numerical stability and accuracy.
dt	-	Time step size, a read-only parameter.

Minimum Mesh Size #

Minimum mesh size setting:

Name	Default	Description
Min mesh size setting	0.00025 $\mu m$	Define the minimum size of a single mesh cell; in general, a smaller minimum mesh size can provide finer resolution, but requires more computational resources. This parameter does not need to be modified under normal conditions.

More Information #

Mesh Order #

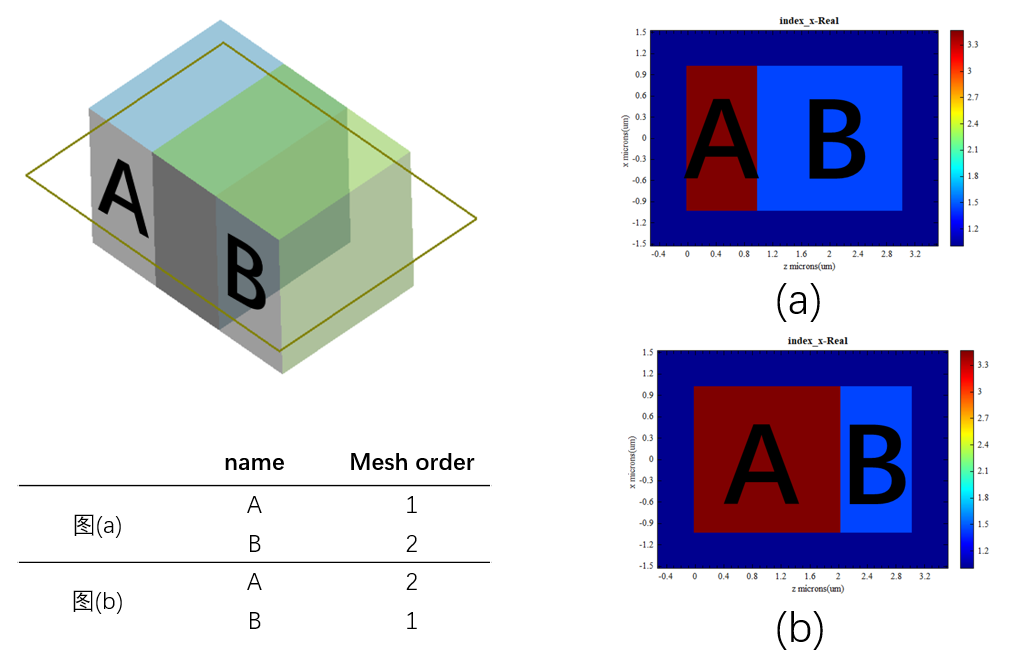
Mesh order is a structural property used to set the order in which meshes are created.

When structures overlap in space, the selection of materials for the overlapping region can be controlled by setting the Mesh order (the larger the Mesh order, the higher the material grade). The specific setting steps are as follows: select a structure, right-click to open the Edit properties window, switch to the Material tab, tick Override mesh order (inactivated by default), and set the number of levels for Mesh order.

By modifying the Mesh order for structure A and structure B, the material selection for the intersecting space is specified, as shown in the figure below.

Case Study 1: Combination Effect of Different Mesh Types and Refinement Methods #

Create a simple model: dielectric sphere project with $\widetilde{N} = 3.472$.

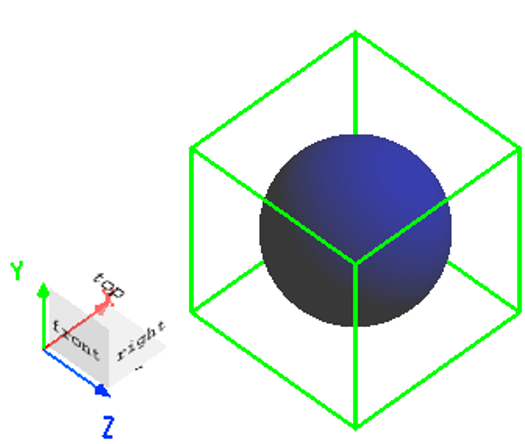
Set up using different mesh types and refinement methods, as shown in the table below:

Name	Mesh type	Mesh refinement	More
$(a)$	Uniform	Staircase	A simpler mesh setting, with higher partitioning efficiency.
$(b)$	Auto nonuniform	Staircase	Efficient and accurate partitioning.
$(c)$	Uniform	Conformal variant VP-EP0	Better modeling effect for devices sensitive to boundaries.

Use View the current material data to see the created results (for a combination of other mesh types and refinement methods, please try it yourself):

Add Index monitor to view the material distribution in the central cross-section.

Case Study 2: Using Semi-auto Nonuniform Mesh #

In general simulations, Auto nonuniform mesh is sufficient for accurate mesh partitioning. The software provides Semi-auto nonuniform mesh for advanced users to customize mesh partitioning.

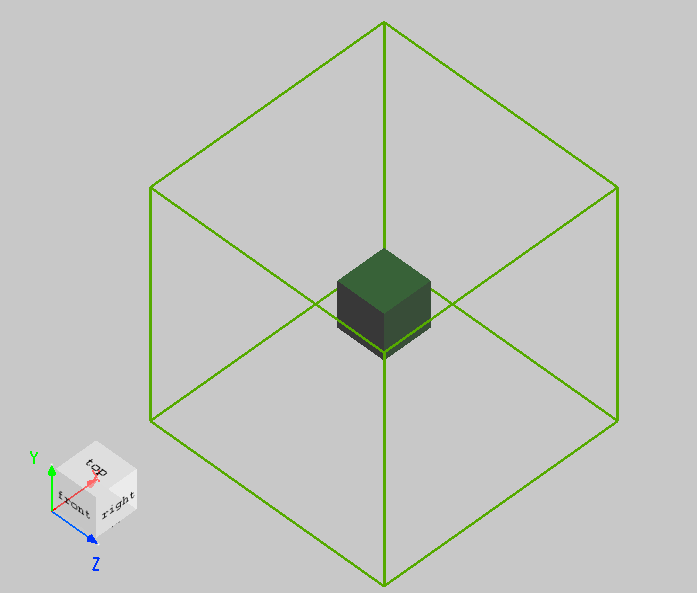
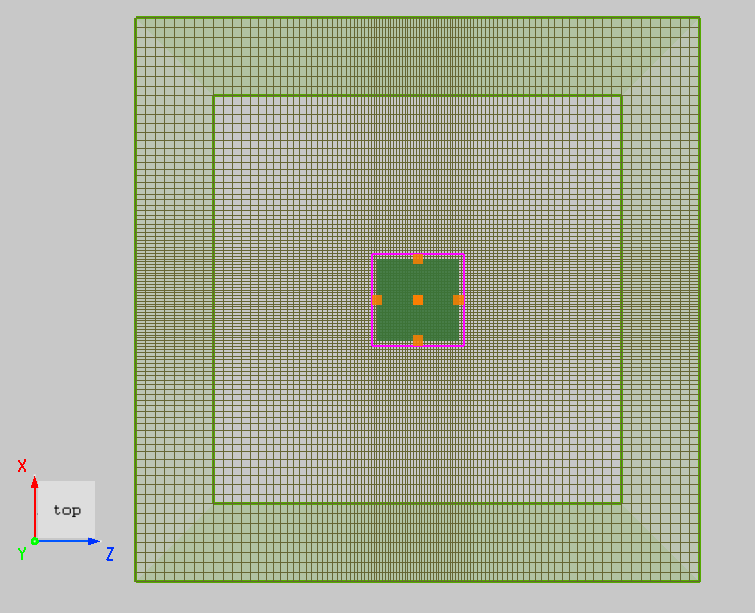
1. Create a simple cube model with a relative refractive index of 4 and a simulation wavelength of $1\mu m$. Using Auto nonuniform mesh with an accuracy level of 2, the mesh size in the vacuum is $0.1\mu m$, and the mesh size in the cube region is $0.025\mu m$. The mesh partitioning is shown below.

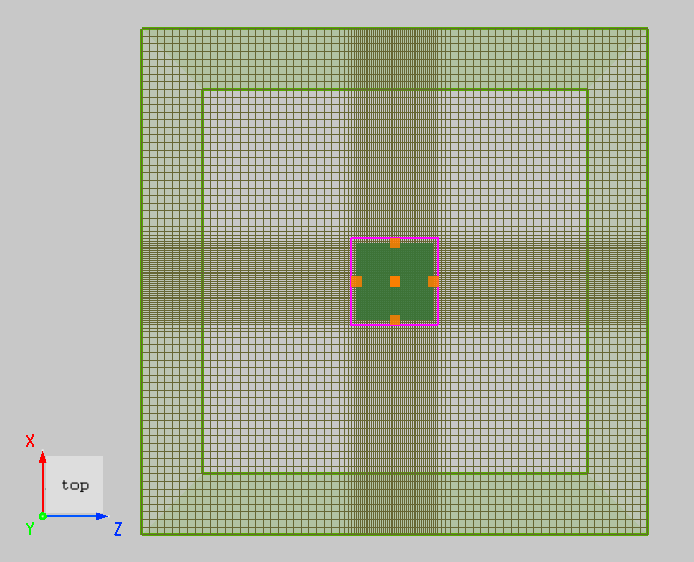
Using Semi-auto nonuniform mesh, the following settings can achieve smoother transitions:

Mesh type	Mesh definition type	Mesh grading factor
Semi-auto nonuniform	Mesh cells per wavelength = 10	1.05

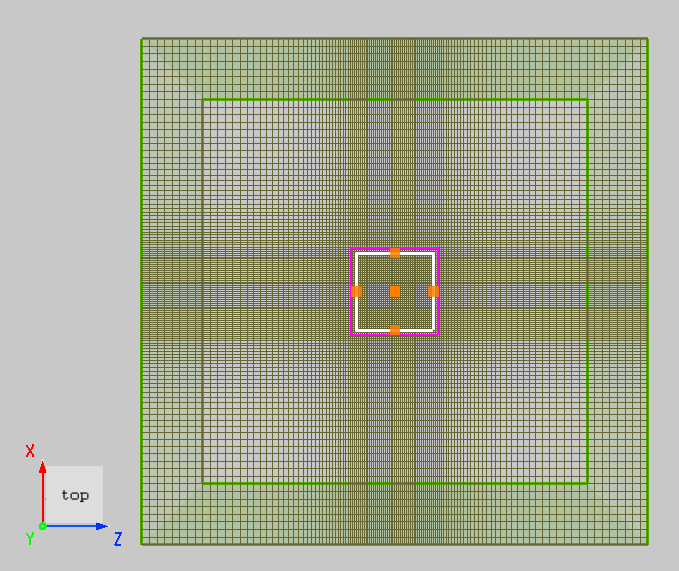
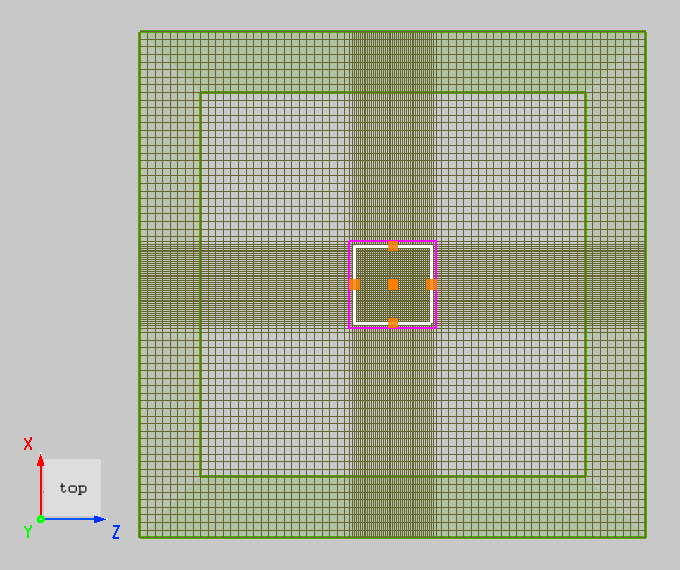
2. Similarly, in large-scale simulations, a larger Mesh grading factor can be used to increase the mesh growth rate and save computational resources. Create a Custom Mesh with $dx=0.025\mu m$, and compare the results using different grading factor values. The first image uses 1.05, and the second image uses 1.8.

Mesh type	Mesh definition type	Mesh grading factor
Semi-auto nonuniform	Mesh size = 0.1 $\mu m$	1.05 / 1.8

Related Publications #

[1] Yu W, Mittra R. A conformal finite difference time domain technique for modeling curved dielectric surfaces[J]. IEEE Microwave and Wireless Components Letters, 2001, 11(1): 25-27.
[2] Taflove A, Hagness S C, Piket-May M. Computational electromagnetics: the finite-difference time-domain method[J]. The Electrical Engineering Handbook, 2005, 3: 629-670.
[3] Zhao Y, Hao Y. Finite-difference time-domain study of guided modes in nano-plasmonic waveguides[J]. IEEE transactions on antennas and propagation, 2007, 55(11): 3070-3077.
[4] Mohammadi A, Nadgaran H, Agio M. Contour-path effective permittivities for the two-dimensional finite-difference time-domain method[J]. Optics express, 2005, 13(25): 10367-10381.