Preface #

Integrated photonics has become a key enabling technology in areas such as optical communications, sensing, and signal processing. Among various photonic devices, microring resonators are widely used in applications such as filtering, modulation, and nonlinear optics due to their compact footprint, high quality factor, and excellent wavelength-selective properties. To achieve the desired spectral response within the target wavelength range, precise parameter optimization and performance prediction are essential during the design stage.

In this case, we design and simulate a microring resonator with a center wavelength of $1.55 \mu m$ and a free spectral range (FSR) of $3200 GHz$.

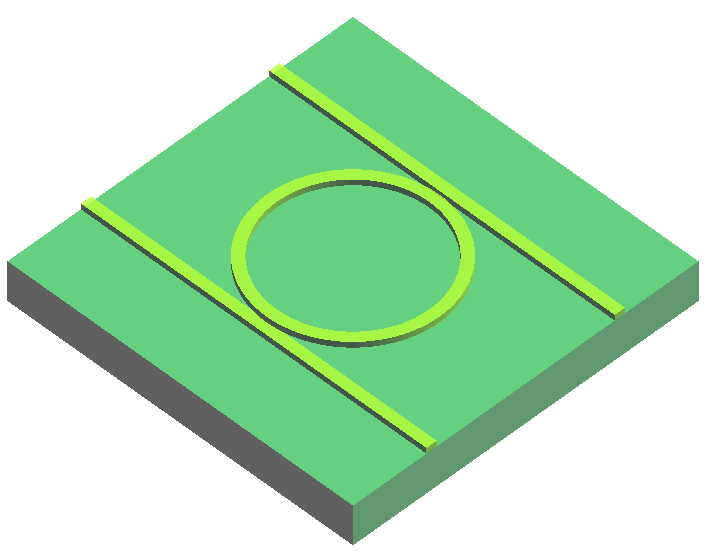
We first use the FDE solver to calculate $n_{eff}$ and $n_g$ and determine an appropriate microring radius. Then, with the radius fixed, a 2.5D FDTD simulation is performed to obtain the transmission spectrum and Q factor from the input port to the drop port. The results are compared with those from a 3D FDTD simulation to verify both the design accuracy and the reliability of the simulation method.

Simulation Settings #

Device introduction #

The model used in this case is shown above, and the waveguide is an SOI structure with dimensions of $0.4 \mu m \times 0.22 \mu m$. The widths of the double straight waveguides ($wg_{width}$) and the microring waveguide ($ring_{width}$) are identical, and the waveguide gap is set to $0.1 \mu m$.

The design goal is to achieve an FSR of $3200 GHz$ (corresponding to a wavelength spacing of $25.6 nm$) at the center wavelength of $1.55 \mu m$. To meet this requirement, the microring radius $R$ must satisfy both of the following equations:

$R=\frac{m \lambda}{2\pi n_{eff}},\space R=\frac{\lambda^2}{2\pi n_g FSR}$

Here, $n_{eff}$ and $n_g$ are the effective index and group index of the guided mode at $1.55 \mu m$, respectively. The first equation arises from the resonance mode condition, ensuring phase coherence after one round trip in the ring. The second equation comes from the relationship between FSR and ring circumference, ensuring the resonance spacing meets the design target.

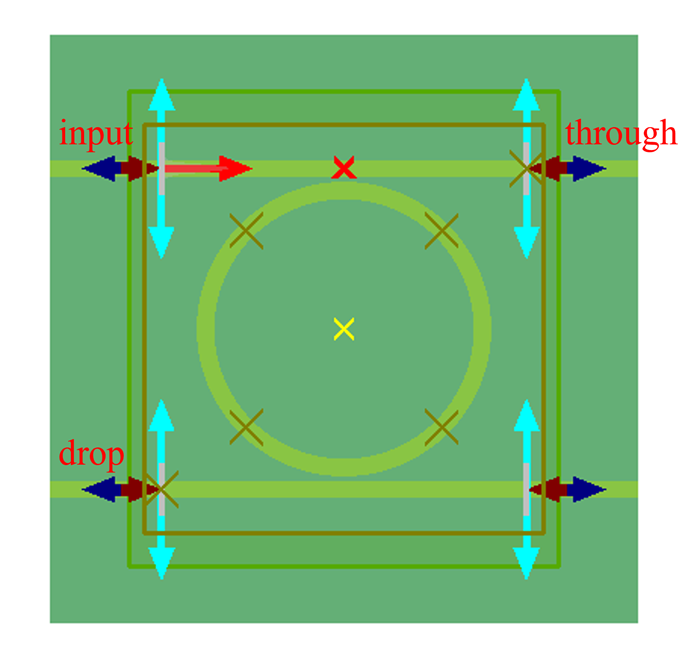
Solver settings #

Since silicon is a dispersive optical material, to ensure continuity of the material model over the frequency range, the sampled material data sampling type in the FDE solver should be set to use a polynomial material model fit.

The ring resonator is a high Q device, and in order to get more accurate simulation results, a longer simulation time is needed, in this case, the FDTD simulation time needs to be set to 5 ps. For the 2.5D FDTD simulation, because the source bandwidth is $0.1 \mu m$ and waveguide dispersion must be considered, the Broad bandwidth option should be enabled in the 2.5D setting tab. The slab position should be set to the location of the waveguide, as described in the 2.5D Solver documentation.

Simulation results #

Effective Index and Group Index #

Open the attached RingResonator_FDE.mpps project and run the neff_ng.msf script to sets up the FDE solver to perform mode solving and frequency sweeping to get the effective index and group index at $1.55 \mu m$.

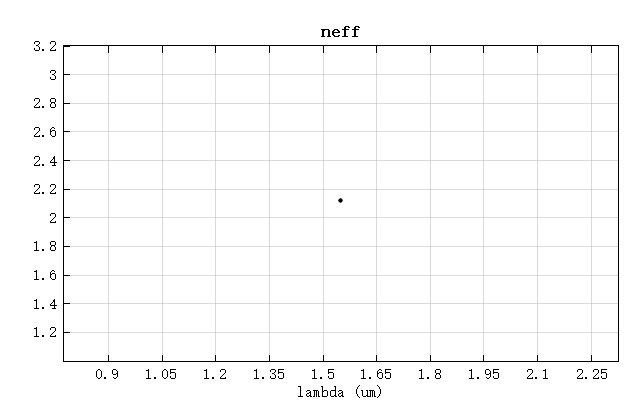
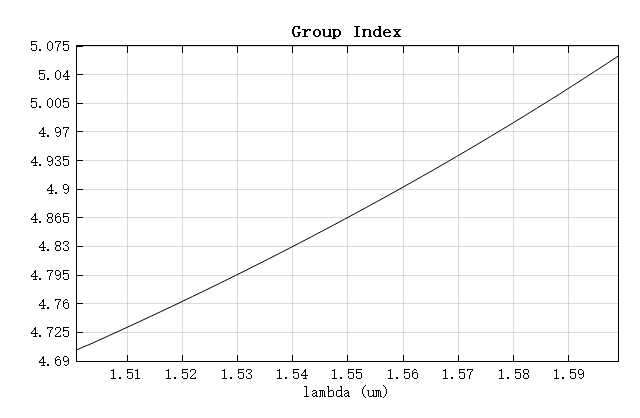
The results show that $n_{eff}=2.1155$ and $n_g = 4.865$. When $m=27$, the radii calculated from the two formulas are closest, corresponding to $R \approx 3.15 \mu m$.

Transmission Spectrum #

Before performing both 2.5D and 3D simulations, the RingResonator_structure.msf script is used to adjust parameters such as the ring radius and port positions. The transmission spectrum obtained from the two simulation methods are presented below.

First, run the RingResonator_2.5d.mpps project. Afterward, use the RingResonator.msf script to obtain the transmission spectrum at the four ports:

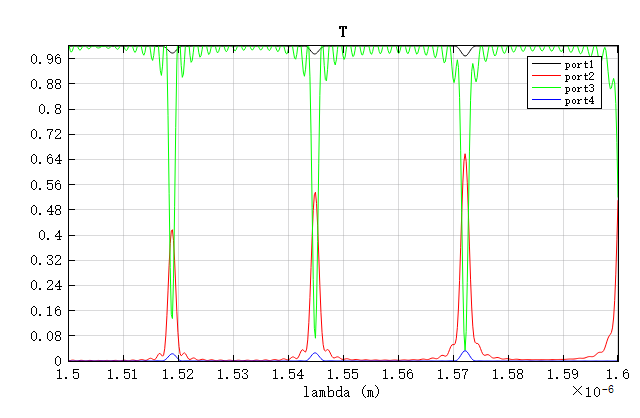
The results show three distinct resonance peaks, with the central wavelength at $1.545 \mu m$, differing from the design value by less than 1%. This confirms the effectiveness of 2.5D FDTD for rapid modeling and analysis.

Subsequently, the RingResonator_3d.mpps project is executed, and the transmission spectrum obtained is shown below:

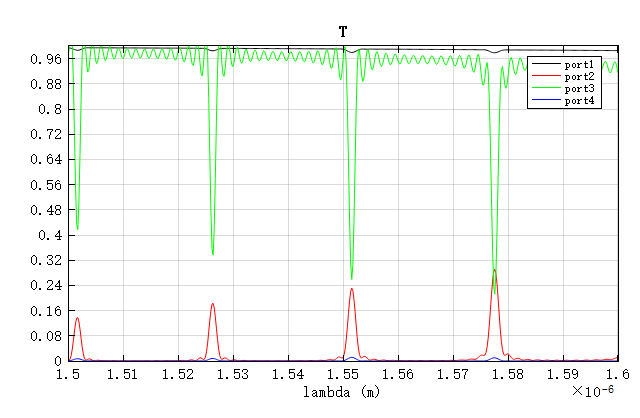
It can be seen that the 3D simulation yields a central wavelength of $1.551 \mu m$, which is closer to the design value than the 2.5D result, demonstrating the superior accuracy of 3D FDTD. The subsequent result analyses are therefore based on 3D simulations.

Electric field distribution at resonant wavelengths #

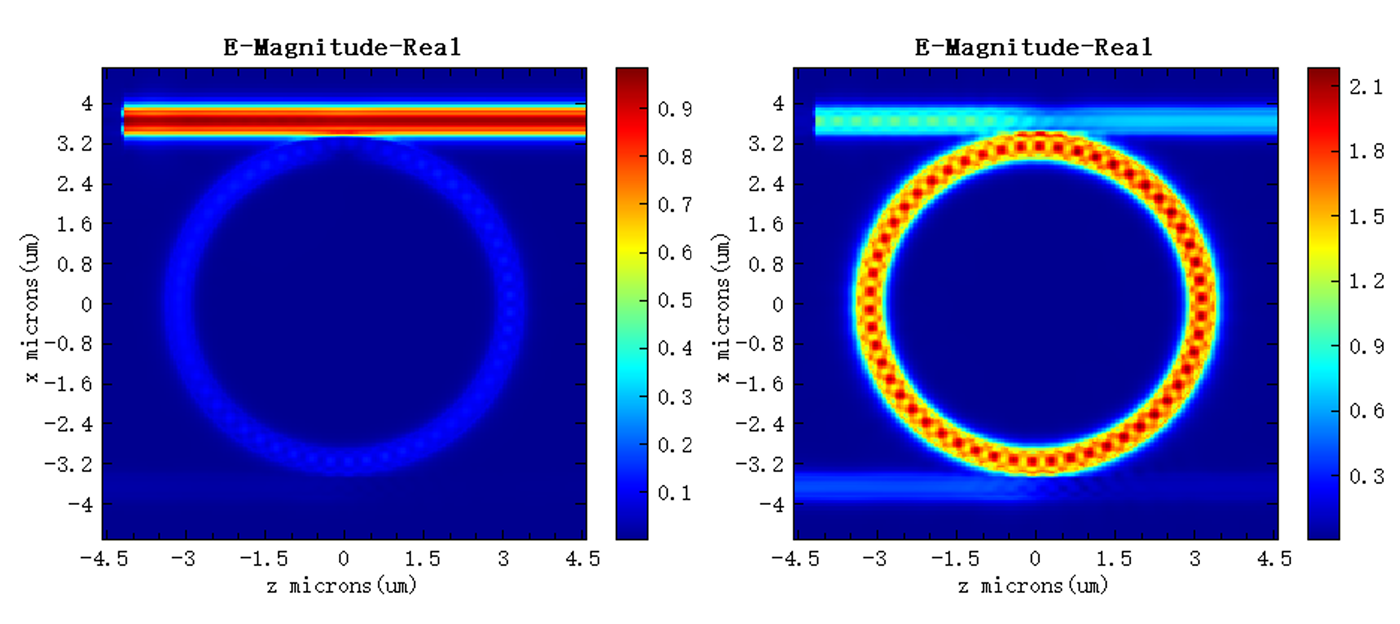
According to the resonance peak at the output port, the data of FDFP monitor ZX were viewed. The electric field intensity at the resonance peaks is shown in the right figure. Clearly, compared with the non-resonant wavelength of $1.54 \mu m$ (left figure), the field intensity is significantly enhanced.

Q factor #

The High Q analysis group in the project computes the Q factors for the three resonance peaks:

[High Q analysis::analysis script result] 
val =
Resonance 1:  
val =
    frequency = 193.219THz, or 1551.57 nm  
val =
    Q = 2471 +/- 0.0192705  
val =
Resonance 2:  
val =
    frequency = 196.43THz, or 1526.21 nm  
val =
    Q = 3257.29 +/- 0.000534521  
val =
Resonance 3:  
val =
    frequency = 190.071THz, or 1577.27 nm  
val =
    Q = 1815.94 +/- 0.127365 

Comparison with theoretical Results #

Using the attached RingResonator.msf script, the theoretical spectrum of the $drop$ port at a center wavelength of $1.55\mu m$ and $FSR=3200GHz$ was calculated and compared with the simulation results, as shown below.

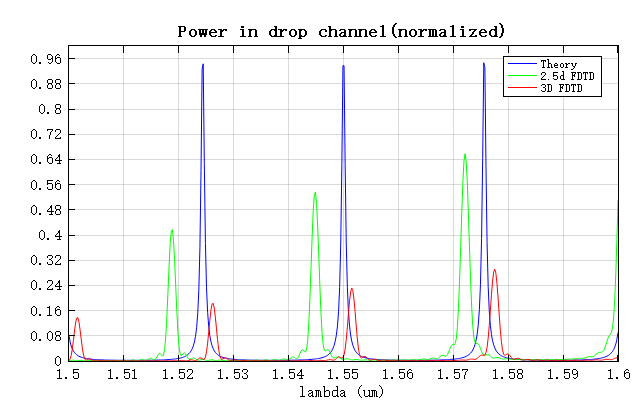
The simulated FSR agrees well with the theoretical value. The overall transmission from the 3D FDTD simulation is lower, mainly because more loss factors are present in the full 3D model. The precise position of the resonance peak is highly sensitive to the effective optical length of the microring resonator. Although both simulation methods use the same structure, the 2.5D simulation requires approximating 3D materials as a 2D model. This approximation introduces a certain degree of error, leading to slight differences in effective optical length compared with the 3D simulation, and consequently a small shift in the resonance peak position.

References #

[1] Mirza, Asif , et al. “Silicon Photonic Microring Resonators: Design Optimization Under Fabrication Non-Uniformity.” Design, Automation and Test in Europe Conference and Exhibition 2020.
[2] Zhou Z P. Silicon based optoelectronics. Peking University Press, 2012.
[3] Hammer, Manfred , K. R. Hiremath , and R. Stoffer . “Analytical Approaches to the Description of Optical Microresonator Devices.” Aip Conference Proceedings (2004).