Preface

Mie scattering is an effect that occurs when particles have a size comparable to or larger than the wavelength of the incident light. The scattered light intensity is asymmetric in various directions, with most of the incident light scattered along the direction of its original propagation. In this case, we use FDTD to calculate the scattering field of a nanoparticle excited by a Total-field Scattered-field(TFSF) light source. The built-in analysis group of far field from a closed box is then employed to compute the far-field scattering distribution of the particle.

Simulation settings

Device introduction

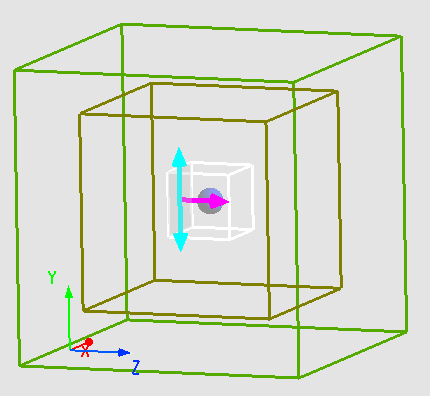
In this case, a TFSF light source is used to excite a dielectric particle with a diameter of $1.06\mu m$ and a refractive index of $n=2$. Since the particle is radially symmetric and the light source is symmetric in the $X$ direction but anti-symmetric in the $Y$ direction, the $X_{min}$ boundary employs a Symmetric condition, while the $Y_{min}$ boundary uses an Anti-symmetric condition.

Source

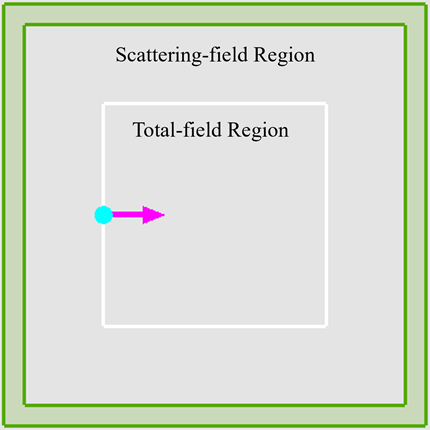
The TFSF light source has two regions: the total field region within the bounding box of the light source and the scattered field region outside the bounding box. The total field includes the incident field and the scattered field. The incident field of the TFSF light source is a plane wave. In the scattered field region, only the scattered field $E_{scat}$ exists. By placing monitors in the scattered field region, we can eliminate the incident field and directly study the scattering field. Since Mie scattering occurs when the particle size is close to the wavelength of the incident light, the TFSF light source uses a wavelength of 1.06μm.

Far field from a closed box

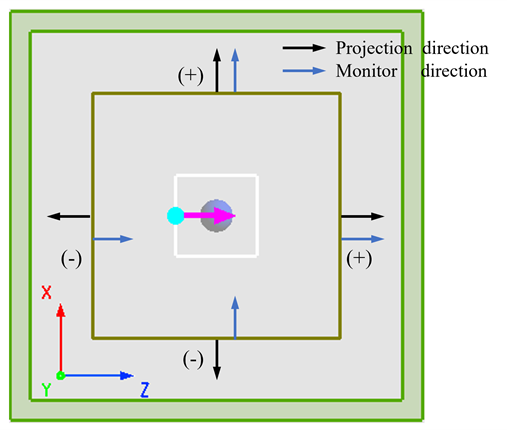
According to the surface equivalence theorem, calculating the far-field projection of a scattering object requires evaluating its near-field contributions in each direction. Therefore, the software includes an analysis group called Far field from a closed box, which uses six FDFP monitors to enclose a closed box and record near-field values in all directions outside the scattering object. By applying the principle of linear superposition, we can determine the field distribution of any scattering object at a specified far-field observation location, effectively achieving the projection from near-field to far-field for arbitrary scatterers.
The linear superposition rule for the far-field projection is illustrated in the diagram below. The outward projection surface normal of the closed box is considered as the positive direction. Therefore, if the outward projection surface normal aligns with the defined direction of the FDFP monitor, the electric/magnetic fields are assigned as positive sign; otherwise, assigned as negative sign.
Note: The box formed by the FDFP monitors must be enclosed, ensuring that all sources and structures are inside the box. There should be no light sources or structures intersecting or passing through the surface of the box.

Simulation results

Near-field result

The FDFP monitors in the analysis group can capture the electric field distribution of the particle's scattered field on the enclosed surfaces. These enclosed surfaces consist of the six faces of the cube. The electric field distributions on these surfaces are then unfolded according to their spatial positions, as shown in the figure below. Symmetric and Anti-symmetric boundary conditions were used in the attachment project, so the $xn$ and $yn$ monitors are not within the simulation region and thus have no simulation results. Their electric field distributions can be symmetrically obtained from the $xp$ and $yp$ monitors, respectively. As shown in the figure, after the light source propagates along the positive $Z$ axis and excites the dielectric sphere, the $zp$ monitor captures the maximum scattered light intensity.

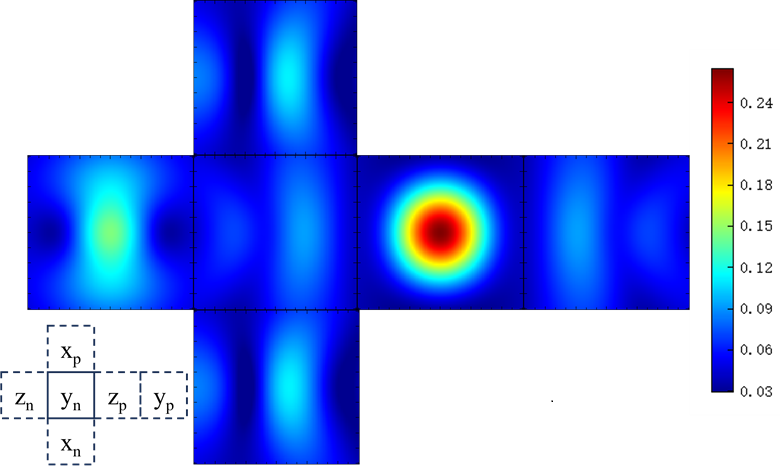
Far-field result

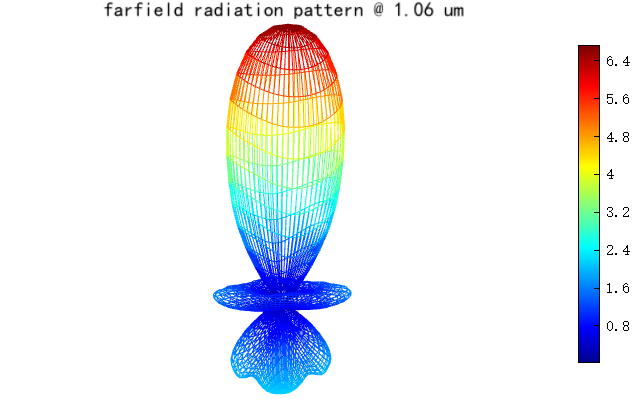
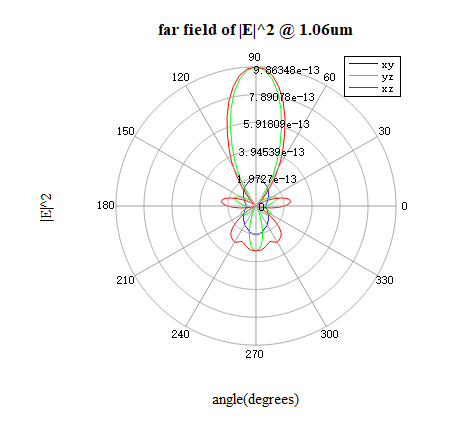
After simulation, run the analysis script of the analysis group to project the near-field data obtained from the FDFP monitor to the far field. By default, the far-field projection is located at a circle with a radius of $1m$. However, this far-field projection can be modified to any spatial location (as long as it satisfies the far-field conditions). The figure below shows the scattered field in the far-field at the $XY、 YZ、 XZ$ planes projected on the circle with a radius of 1m. Notably, the strongest scattering occurs in the positive $Z$ direction, which matches with the characteristic of Mie scattering where the scattering field predominantly concentrates along the positive direction of light propagation.

Running the attached script will generate a three-dimensional far-field radiation pattern for Mie scattering of the dielectric sphere. The result also visually reveals that the scattering direction of the sphere predominantly aligns with the positive $Z$ axis.