如何使用“对称”和“反对称边界”减少仿真空间？如何判断自己设置的“对称”和“反对称边界”是否准确？ #

问题描述 #

在设置求解器时，我希望通过设置对称和反对称边界条件来减少仿真空间，提高计算效率。但是我不确定什么情况下可以使用这些边界条件，以及如何正确地进行设置。

可能的原因 #

用户在使用对称性边界条件时，需准确理解以下两点：

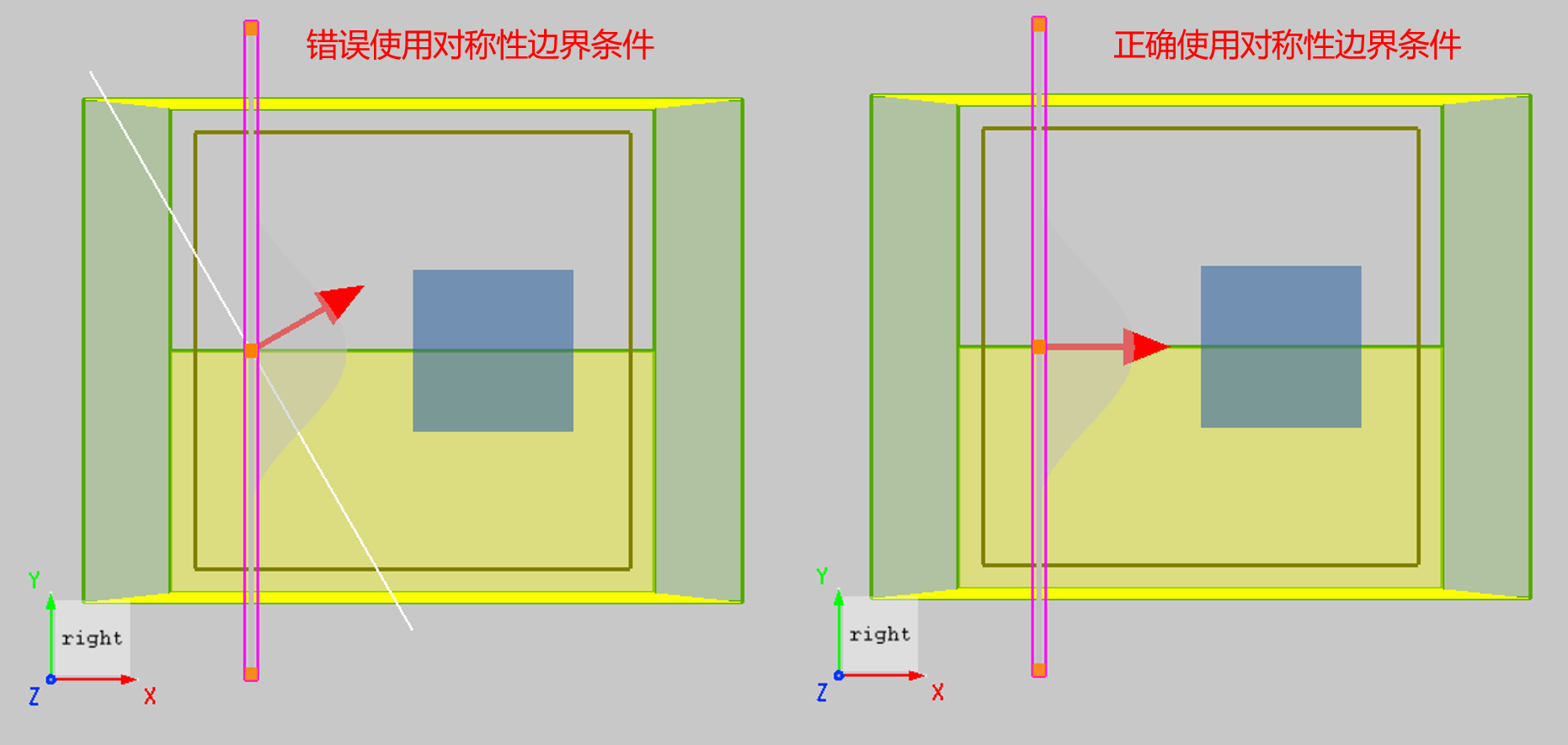
1.适用场景：对称性边界条件主要用于节省计算空间、降低内存占用并加速仿真。使用时，要求物理结构（几何与材料）对称，同时光源的场分布也需满足对称性。如下图所示，若光源为斜入射，则不满足对称性要求，无法使用对称性边界条件；而垂直入射且场分布关于对称平面对称时，则可以使用。合理利用对称性，可在每个方向上将计算区域缩减一半，从而显著提升仿真效率。

2.实现原理：对称/反对称边界条件通过在麦克斯韦方程组中，将对称平面上的特定场分量强制设为零来实现。下表列出了每种边界条件下为零的场分量。在仿真中，我们只需关注对称平面上不为零的光源场分量，即除下表所列分量之外的分量。

	对称边界条件	反对称边界条件
法向电场分量	0
切向电场分量		0
法向磁场分量		0
切向磁场分量	0

解决方案 #

问题排查 #

在使用对称/反对称边界条件时，用户容易误选错误的边界类型。若选择错误，系统不会发出警告，但仿真结果会出现严重偏差。验证方法：可先进行一次不使用对称性边界条件的仿真，再与使用对称性边界条件的仿真结果进行对比。如果两次结果一致，说明设置正确；否则，可能存在设置错误。

解决方法 #

对称/反对称边界条件旨在提升具有对称性的仿真工程的计算效率，属于软件的高级功能。关于其正确使用方法，请参考以下要点。若仍有疑问，请联系我们。

1. 对称性边界条件需遵循一定的对称规则。电磁场在不同对称性边界条件下的分布规律如下，具体可参考对称/反对称。

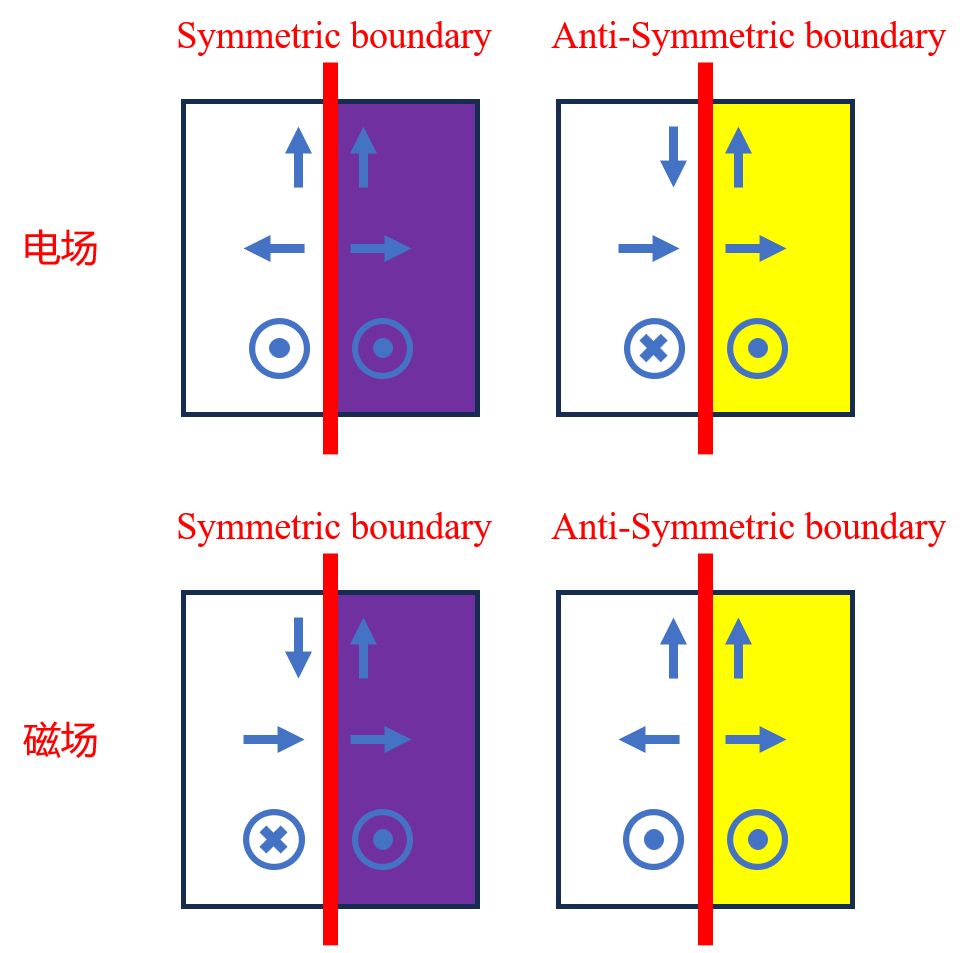
上述规则在模式源求解及腔体谐振模式研究时非常有用。如下图所示，$E_y$分量以向右为正方向，图中该分量在各部分均为正值；$E_z$分量在各部分的符号都与相邻部分相反。结合上述规则，可以确定，在Y=0处存在一个反对称平面，Z=0处存在一个对称平面。因此可将y min设置为反对称边界，z min设置为对称边界。

2. 在x/y/z方向上的min/max边界设置不同的对称性边界条件，会产生不同的效果。当某一侧边界使用对称性边界条件时，等效于采用对侧边界条件，同时节省一半的仿真空间；当同一方向两侧边界均使用对称性边界条件时，等效为周期边界条件（即空间中拥有无限个仿真周期）。
如下图所示，a、b两种设置应当等效。需要注意的是，该方向具体应采用对称边界条件还是反对称边界条件，需要根据光源的电磁场在对称平面处的分布才能确定。

• 当仿真工程使用周期边界条件，将该方向的边界替换为同类型的对称性边界，两者结果完全等效；
• 当仿真工程使用PML边界条件，将对称性方向单侧边界替换为对称性边界条件，两者结果也完全等效。

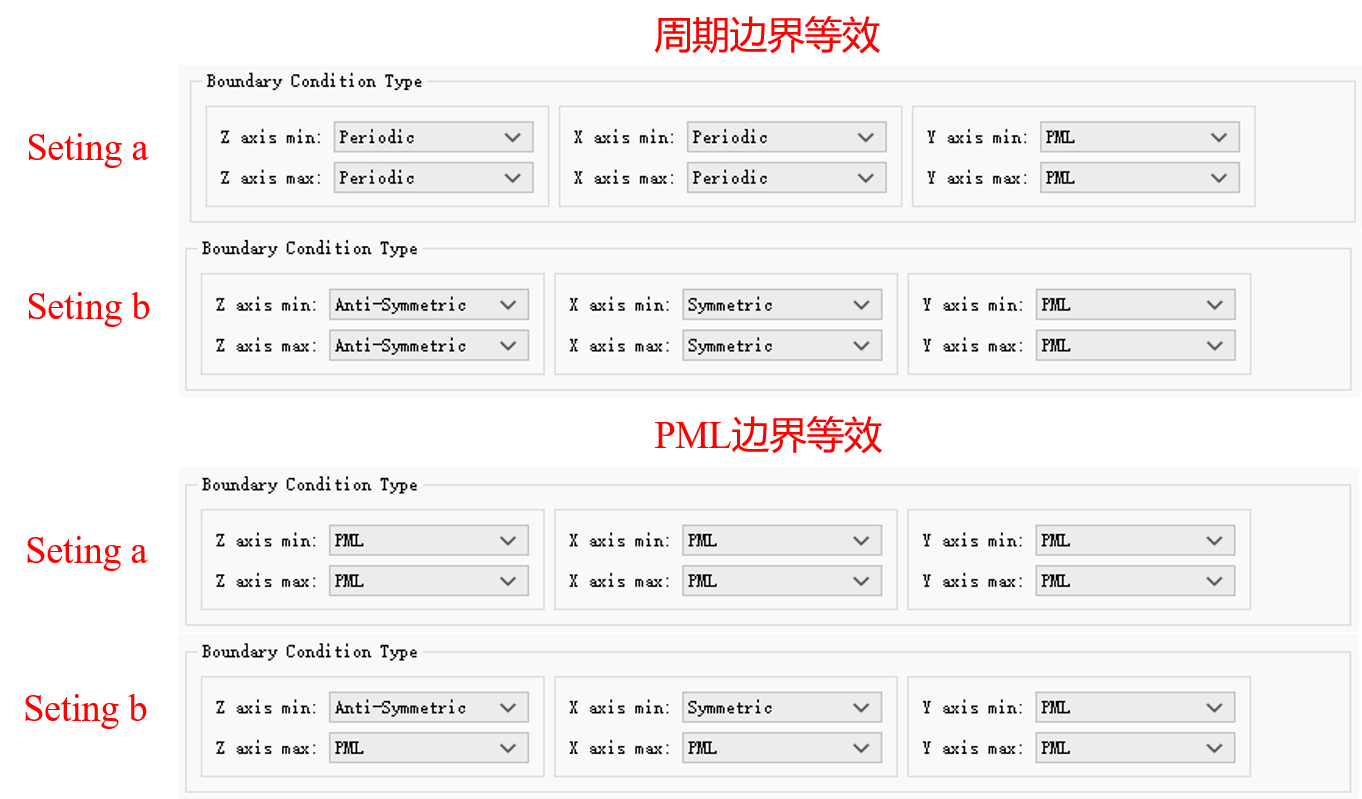
以上两种替换方法，均可将计算区域缩减至原始尺寸的1/4。需要注意：同一方向上的min/max边界，不能一边设置为对称边界条件，另一边设置为反对称边界条件。

除上述规则外，用户在使用对称性边界条件时还需注意以下事项：

• 在使用对称性边界条件后，请勿再更改仿真区域大小。此时仿真区域对应方向的一半将会以紫色或黄色阴影显示，表示该区域不会被直接仿真。
• 仿真完成后，监视器内的场数据会根据对称规则自动展开。即使实际仿真只模拟了半个区域，也能绘制整个仿真区域的电磁场分布。需要注意，部分分析组可能无法正常工作。

相关阅读 #

对称/反对称